Page 111 - 应用声学2019年第2期

第 38 卷 第 2 期 李均浩等： 一种改进的非整数自适应时延估计方法 257

输入信号，LMPFTDE算法的代价函数为多峰函数， 值整数位估计，将得到的估计值，作为 LMPFTDE
直接进行迭代算法可能不收敛，迭代值在D−0.5与 算法时延值迭代的初值。最后进行自适应时延估计，
D+0.5之间(D 为时延真值)，代价函数是单峰的，所 求出更高分辨率的时延估计值。改进的非整数自适
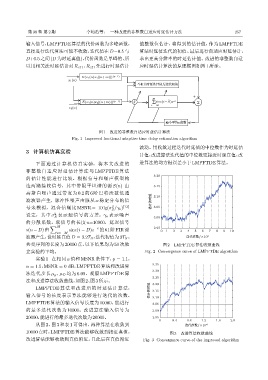
以用相关法时延估计对 R c11 、R c21 先进行时延估计 应时延估计算法的原理框图如图1所示。

Eıx 1↼n↽x 1♭↼n⇁m↽♯℘ ↼p֓↽
x 1↼n↽
̉ᄱТ௑णͥᝠϙ˞ᤖ̽Ѻϙ

+
M -
^
Eıx 1↼n↽x 2♭↼n⇁m↽♯℘ ↼p֓↽ g ⌣ ∑ sinc↼i֓D↽z −i ∑
i/−M
x 2↼n↽
త࠵ࣱکpᔵ஝

图 1 改进的非整数自适应时延估计算法
Fig. 1 Improved fractional adaptive time delay estimation algorithm
波动。用收敛过程迭代时延值的中位数作为时延估
3 计算机仿真实验
计值，改进算法迭代值的中位数更接近时延真值，改

下面通过计算机仿真实验，将本文改进的 进算法的均方根误差小于LMPFTDE算法。
非整数自适应时延估计算法与 LMPFTDE 算法
3.20
的估计性能进行比较。根据信号和噪声模型构
造两路接收信号，其中带限平坦谱的源 S(n) 由 3.15
高斯白噪声通过带宽为 0.2 的 6 阶巴特沃兹低通 3.10
滤波器产生，脉冲性噪声由服从 α 稳定分布的信 ͥᝠᄊ௑ण
2
号来模拟，混合信噪比 MSNR = 10 lg(σ /γ v ) [13] 3.05
S
2
设定，其中 σ 表示源信号的方差；γ v 表示噪声
S 3.00
的分散系数，取信号的长度 n=10000，延迟信号
∑ M
s(n − D)由 sinc(i − D)z −i 的61阶FIR滤 2.95 0 1 2 3 4 5 6 7 8 9 10
i=−M
波器产生，设时延真值D = 3.2T S ，迭代初值为3T S 。 ᤖ̽൓஝/T10 3
共变序列的长度为 20000 点，以下结果均为 50 次独 图 2 LMPFTDE 算法收敛曲线
立实验的平均。 Fig. 2 Convergence curve of LMPFTDE algorithm
实验 1 在相同 α 值和 MSNR 条件下，p = 1.1，
α = 1.5，MSNR = 0 dB，LMPFTDE算法和改进算 3.35
3.30
法迭代步长 µ g 、µ D 均为 0.09。观察 LMPFTDE 算
3.25
法和改进算法收敛曲线，如图2、图3所示。 3.20
LMPFTDE 算法和改进后的时延估计算法， ͥᝠᄊ௑ण 3.15
输入信号的长度表示算法能够进行迭代的次数。 3.10
LMPFTDE 算法的输入信号长度为 10000，能进行 3.05
的最多迭代次数为 10000；改进算法输入信号为 3.00
20000，能进行的最多迭代次数为20000。 2.95
0 0.4 0.8 1.2 1.6 2.0
从图 2、图 3 和表 1 可得出，两种算法在收敛到 ᤖ̽൓஝/T10 4
10000 点时，LMPFTDE 算法能够收敛到接近真值， 图 3 改进算法收敛曲线
改进算法能够收敛到真值附近，且此后在真值附近 Fig. 3 Convergence curve of the improved algorithm