Page 112 - 应用声学2019年第2期
P. 112
258 2019 年 3 月
表 1 LMPFTDE 算法和改进算法的估计性能比较 中,改进算法在 −5 dB 到 8 dB 的最低均方误差均
Table 1 Performance comparison on LMPF- 低于 LMPFTDE 算法的最低均方误差,改进算法
TDE algorithm and the improved algorithm 的时延收敛因子与信噪比迭代步长为0.19。在不同
信噪比下,改进算法的最低均方根误差均要低于
LMPFTDE 算法 改进算法
LMPFTDE 算法,但其不在一条折线上。表明参数
估计的偏差 −0.0917 −0.0666
的选择对算法性能有很大影响,在不同环境下选用
估计的方差 0.0049 0.0055
合适的参数,能够获得更好的估计效果。
估计值 (中位数) 3.1191 3.1596
实验 3 相同 MSNR、 不同 α 值条件下, 比
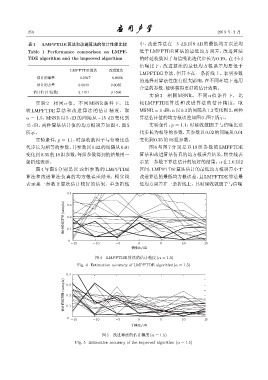
实验 2 相同 α 值、 不同 MSNR 条件下, 比 较 LMPFTDE 算法和改进算法的估计精度。取
较 LMPFTDE 算法和改进算法的估计精度。取 MSNR = 0 dB,α 以0.2的间隔从1.2变化到2,两种
α = 1.5,MSNR 以 5 dB 的间隔从 −15 dB 变化到 算法估计值的均方根误差如图6、图7所示。
15 dB,两种算法估计值的均方根误差如图 4、图 5 实验条件:p = 1.1,时延收敛因子与信噪比迭
所示。 代步长为相等的参数,其参数以 0.02 的间隔从 0.01
实验条件:p = 1.1,时延收敛因子与信噪比迭 变化到0.35的18组参数。
代步长为相等的参数,其参数以 0.02 的间隔从 0.01 图 6 与图 7 分别是以 18 组参数的 LMPFTDE
变化到0.35 的18组参数,每组参数得到的结果用一 算法和改进算法仿真的均方根误差结果,粗实线表
条折线表示。 示某一参数下算法估计的较好的结果。α 在1.6 到2
图 4 与图 5 分别是以 18 组参数的 LMPFTDE 区间,LMPFTDE算法估计的最低均方根误差小于
算法和改进算法仿真的均方根误差结果,粗实线 改进算法的最低均方根误差,且LMPFTDE算法最
表示某一参数下算法估计较好的结果。单条折线 低均方误差在一条折线上,其时延收敛因子与信噪
0.4
ͥᝠᄊکவಪ (sample) 0.2
0.3
0.1
0
-15 -10 -5 0 5 10 15
η٪උ/dB
图 4 LMPFTDE 算法的估计精度 (α = 1.5)
Fig. 4 Estimation accuracy of LMPFTDE algorithm(α = 1.5)
0.4
ͥᝠᄊکவಪ (sample) 0.3
0.2
0.1
0 -15 -10 -5 0 5 10 15
η٪උ/dB
图 5 改进算法的估计精度 (α = 1.5)
Fig. 5 Estimation accuracy of the improved algorithm (α = 1.5)