Page 58 - 应用声学2019年第2期

204 2019 年 3 月

系数 σ 采用 10 个数据的标准差来定义，表示非线性 间隔 5.4 µs 可判定两波包分别为发射探头的直入
超声检测系数在各个检测位置的波动情况。 射和试块的二次反射波信号，只需截取直入射信号
10 做非线性系数分析。图 7(c)、图 7(d) 的检测信号频
1 ∑
µ = × k i , (5) 谱分析显示基波和二次谐波的最大幅值分别位于
10
i=1
v 2.5 MHz 和 5 MHz 附近，两区域提取的基波信号幅
u 10
#
#
u 1 ∑ 2 度基本相同，而 35 区域的二次谐波幅度是 12 区
σ = t (x i − µ) . (6)
10 域的1.53倍，缺陷区域的相对非线性超声系数更大。
i=1
区域检测法中的接收探头轮换接收位置具有 按区域检测法提取各检测区域 10 个非线性超
′
以下三个作用：(1) 避免试样表面状态、内部结构的 声检测信号，并据式 (4) 求解相对非线性系数 β 。
#
#
局部差异对非线性超声检测信号的影响；(2) 可测 图 8(a) 为在 12 检测区域和 35 检测区域测得的
#
量该区域非线性系数的波动情况，丰富了检测特征 非线性系数随检测位置的变化趋势图，35 检测区
值；(3)区域检测较之逐点扫描检测具有更高的检测 域测得的非线性系数及其波动整体比 12 # 检测区
效率。 域大；图 8(b) 为两检测区域的非线性系数平均值及
非线性波动系数对比，35 # 检测区域的非线性系数
#
3 缺陷的检测信号与特征参数分析 平均值和非线性波动系数分别是 12 检测区域的
1.82倍和11.68 倍。分析原因，缺陷破坏了材料结构
3.1 检测信号及其特征分析 均匀性，导致探头在区域内 N1∼N5 位置处接收到
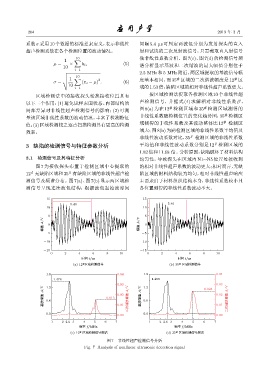
图 7 为接收探头布置于检测区域中心提取的 的相对非线性超声系数的波动更大；相对而言，无缺
#
#
12 无缺陷区域和 35 有缺陷区域的非线性超声检 陷区域的材料结构较为均匀，相对非线性超声响应
测信号及频谱分布。图 7(a)、图 7(b) 显示两区域检 主要来自于材料组织结构本身，非线性系数较小且
测信号呈现连续波包结构，根据波包起始波时间 各位置测得的非线性系数波动不大。

15 15
5.40 5.40
10 10
5 5
ࣨϙ A/V 0 ࣨϙ A/V 0

-5 -5
-10 -10

-15 -15
0 2 4 6 8 10 0 2 4 6 8 10
௑ᫎ t/µs ௑ᫎ t/µs
#
#
(a) 12 ӝ۫ೝ฾ηՂ (b) 35 ӝ۫ೝ฾ηՂ
1.8 0.04 1.8 0.04
1.478 1.488
0.03 1.2 0.023 0.03
۳ฉࣨϙ A/V 0.6 0.015 0.02 ̄൓ៈฉࣨϙ A/V ۳ฉࣨϙ A/V 0.6 0.02 ̄൓ៈฉࣨϙ A/V
1.2

0.01
0.01
0.0 0.0
0.00 0.00
1 2 2.5 3 4 5 6 7 1 2 2.5 3 4 5 6 7
ᮠဋ f/MHz ᮠဋ f/MHz
(c) 12 ӝ۫ೝ฾ηՂᮠ៨ (d) 35 ӝ۫ೝ฾ηՂᮠ៨
#
#
图 7 非线性超声检测信号分析
Fig. 7 Analysis of nonlinear ultrasonic detection signal