Page 59 - 应用声学2019年第2期

第 38 卷 第 2 期 陈振华等： 微小层片型缺陷的超声非线性区域检测技术 205

1.5 1.5 1.5
᭤ጳভጇ஝ࣱکϙ 1.23T10 -2 1.13T10 -3
᭤ጳভฉүጇ஝
ᄱࠫ᭤ጳভጇ஝ β ∋/10 -2 1.2 12 ӝ۫ ᭤ጳভጇ஝ࣱکϙ µ/10 -2 1.0 6.72T10 -3 1.0 ᭤ጳভฉүጇ஝ σ/10 -3

#
0.9
35 ӝ۫
#
0.5
0.5
9.67T10 -5
0.6
0 0
1 2 3 4 5 6 7 8 9 10 12 35
ೝ฾ͯᎶ N ೝ฾ӝ۫
(a) ᄱࠫ᭤ጳভጇ஝ᬤೝ฾ͯᎶᄊԫӑ (b) ᄱࠫ᭤ጳভጇ஝ࣱکϙԣฉүጇ஝
#
#
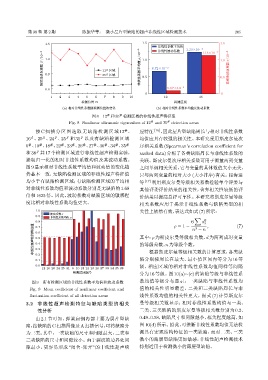
图 8 12 和 35 检测区域的非线性超声特征值
Fig. 8 Nonlinear ultrasonic eigenvalues of 12 # and 35 # detection areas
#
按 C 扫描分区图选取无缺陷检测区域 12 、 应特征 [16] ，因此层片型缺陷周长与相对非线性系数
#
16 、20 、24 、25 和 31 以及有缺陷检测区域 均值应具有较强的相关性。本研究采用斯皮尔曼次
#
#
#
#
#
#
#
#
#
#
#
#
#
6 、10 、18 、22 、23 、26 、27 、30 、34 、35 # 序相关系数 (Spearman’s correlation coefficient for
#
和 38 共 17 个检测区域进行非线性超声检测实验， ranked data) 分析了各类缺陷周长与非线性系数的
提取归一化的相对非线性系数均值及其波动系数。 关联。斯皮尔曼次序相关系数可用于衡量两列变量
图9显示相对非线性系数平均值和波动值的变化趋 之间单调相关关系，它与变量的具体数值大小无关，
势基本一致，无缺陷检测区域的非线性超声特征值 只与两列变量的相对大小 (大小排序) 有关。程海进
均小于有缺陷检测区域；有缺陷检测区域的平均相 等 [17] 利用斯皮尔曼等级相关系数检验单个评委与
对非线性系数均值和波动系数分别是无缺陷的1.68 其他评委评价结果的相关性，舍弃相关性较低的评
倍和 1625 倍。因此，波动系数对缺陷区域的敏感程 价结果以提高总评可靠性。本研究将斯皮尔曼等级
度比相对非线性系数均值更大。 相关系数应用于揭示非线性系数与缺陷类型的相
1.0 关性上依然有效，表达式如式(7)所示：
ฉүጇ஝ σ
0.9 ᭤ጳভጇ஝کϙ µ ∑
d
0.8 ρ = 1 − 6 n − n 2 , (7)
i
᭤ጳভᡔܦೝ฾ྲढ़ϙ 0.6 其中：ρ 为斯皮尔曼等级相关数，d 为两列成对变量
0.7
3
0.5
0.4 的等级差数，n为等级个数。
0.3
根据斯皮尔曼等级相关数的计算要求，各类缺
0.2
0.1 陷分别按周长在最大、最小值区间内等分为 16 等
0.0 级，相应区域的相对非线性系数均值同样等间隔
12 16 20 24 25 31 6 10 18 22 23 26 27 30 34 35 38
ೝ฾ӝ۫ᎄՂ 分为 16 等级。图 10(a)∼(c) 的缺陷等级与非线性系
图 9 所有检测区域的非线性系数平均值和波动系数 数均值等级分布显示：一类缺陷与非线性系数均
Fig. 9 Mean coefficient of nonlinear coefficient and 值的相关性明显最差，二类和三类缺陷周长与非
fluctuation coefficient of all detection areas 线性系数均值的相关性更大。据式 (7) 计算斯皮尔
3.2 非 线 性 超 声 检 测 特 征 与 缺 陷 类 型 的 相 关 曼等级相关数显示：相对非线性系数均值与一类、
性分析 二类、三类缺陷的斯皮尔曼等级相关数分别为 0.2、

由 2.1 节可知，弹簧扁钢内部主要为层片型缺 0.49、0.58，缺陷尺寸和间隙越小，相关程度越高，如
陷，按缺陷的C扫描图像及A扫描信号，可将缺陷分 图 10(d)所示。据此，可推断非线性系数均值无法检
为三类；其中，一类缺陷的尺寸和间隙最大，二类和 测具有宏观结构特征的一类缺陷，而对二类、三类
三类缺陷的尺寸和间隙较小。由于裂纹的边界处间 微小的薄层型缺陷更加敏感，非线性超声检测技术
隙最小，更容易形成 “闭合 -张开” 的非线性超声响 特别适用于检测微小的薄层型缺陷。