Page 73 - 应用声学2019年第2期

第 38 卷 第 2 期 毛燕蓉等： 微型扬声器摆动模态对其辐射声场的影响 219

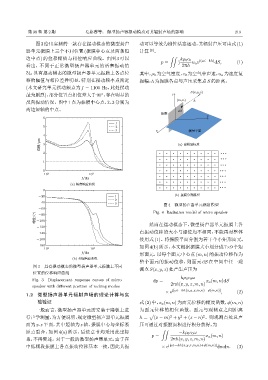
图3 给出实测的一款存在摆动模态的微型扬声 动可以等效为刚性活塞运动，其辐射声压可由式(1)
器单元振膜上三个不同位置 (振膜中心点及两条短 计算 [9] 。
边中点) 的位移幅值与相位响应曲线。由图 3 可以 ∫∫ kρ 0 c 0 j(ωt−kh)
p = j u a e dS, (1)
看出，不同于正常微型扬声器单元的活塞振动情 2πh
况，具有摆动模态的微型扬声器单元振膜上各点位 其中，ρ 0 为空气密度，c 0 为空气中声速，u a 为速度复
移的幅值与相位差异明显，特别在摆动频率点附近 振幅，h为振膜各点与声压采集点S 的距离。
(本文研究单元摆动频点为 f = 1100 Hz，此处摆动
S↼x֒y֒z↽
最为剧烈)，部分位置点相位差大于90 ，存在明显的 z
◦
反向振动情况。图中 1 点为振膜中心点，2、3 分别为 ↼m֒n↽ h
两边短轴的中点。 dS
૝ᒛ
y
6
1
5 2
3 x ฾᧚ࣱ᭧
4
ͯረ/mm 3 (a) थവگಖጇ

2
1

0
10 2 10 3
f/Hz
(a) ࣨए־ऄజጳ
0
-20 1 (b) ૝ᒛѬҟവی
2
-40
3 图 4 微型扬声器单元辐射模型
-60 Fig. 4 Radiation model of micro speaker
ᄱͯ/(O) -100
-80
-120 然而在摆动模态下，微型扬声器单元振膜上各
点振动位移的大小与相位均不相同，不能再对整体
-140
-160 使用式 (1)。将振膜平面分割为若干个小矩形面元，
-180 如图 4(b) 所示，本文根据振膜大小划分成 7×9 个矩
10 2 10 3
f/Hz
形面元，以每个面元中心点 (m, n) 的振动位移作为
(b) ᄱͯ־ऄజጳ
整个面元的振动位移，则面元 dS 在空间中任一观
图 3 具有摆动模态的微型扬声器单元振膜上不同
测点S(x, y, z)处产生声压为
位置的位移响应曲线
kρ 0 c 0 ω
Fig. 3 Displacement response curves of micro dp = − x a (m, n)dS
2πh(x, y, z, m, n)
speaker with different position of rocking modes
× e j[ωt−kh(x,y,z,m,n)−ϕ(m,n)] , (2)
1.2 微型扬声器单元辐射声场的理论计算与实
验验证 式(2) 中，x a (m, n) 为面元位移的幅度函数，ϕ(m, n)
一般而言，微型扬声器单元需安装于障板上进 为面元位移的相位函数。面元与观测点之间距离
√
行声学测量，为方便说明，规定微型扬声器单元振膜 h = (x − m) + y + (z − n) 。则观测点处总声
2
2
2
面为 x-z 平面，其中短轴为 z 轴，振膜中心与坐标系 压可通过对振膜面积进行积分获得，为
原点重合，如图 4(a) 所示，后续章节均采用此坐标 ∫∫ −kρ 0 c 0 ω
p = x a (m, n)
系，不再赘述。对于一般的微型扬声器单元，由于在 2πh(x, y, z, m, n)
中低频段振膜上各点振动位移基本一致，因此其振 × e j[ωt−kh(x,y,z,m,n)+ϕ(m,n)] dmdn. (3)