Page 74 - 应用声学2019年第2期

220 2019 年 3 月

对式(3)进行离散化，则观测点声压p为 SPL(f)
(
−kρ 0 c 0 ω
∑ ∑
p = x a (m, n) = 20 lg 1 ∑ ∑ −kρ 0 c 0 ω
2πh(x, y, z, m, n) x a (m, n)
m n p Ref 2πh (x, y, z.m, n)
m n
× e j[ωt−kh(x,y,z,m,n)+ϕ(m,n)] ∆m∆n. (4) )
× e j[−kh(x,y,z,m,n)+ϕ(m,n)] ∆m∆n , (5)
为验证上述理论计算的准确性，针对一普通微
型扬声器单元 (产品规格 1511，后续均采用此款单 式 (5) 中，p Ref = 2 × 10 −5 Pa 为参考声压。根据测
元，不再赘述)，不失一般性地随机选取声场中任意 量位移和式 (5) 分别计算并作出绕短轴摆动的微型
三点 (本文选取的三点分别为 (−7, −2, 5)，(6,4,2)， 扬声器单元与正常微型扬声器单元的声压频率响
(0,1,4)，单位为 cm) 进行声压测试并与理论计算进 应进行对比，如图6所示(具有摆动的微型扬声器单
行对比。图 5 给出实测频响曲线与计算频响曲线的 元实测频响曲线同步绘于图中)。
对比。由图 5 可以看出，采用本节所述方法进行的
100
微型扬声器单元辐射声场的理论计算与实测吻合 95 ୌүӭЋ
90 ൤࣢ӭЋ
良好，理论符合实际。 85 ࠄ฾ᮠ־
80
SPL/dB
110 75
ࠄ฾ᮠ־ 70
100
ᝠካᮠ־ 65
60
90
SPL/dB 80 55
50
70 45
10 2 10 3
f/Hz
60
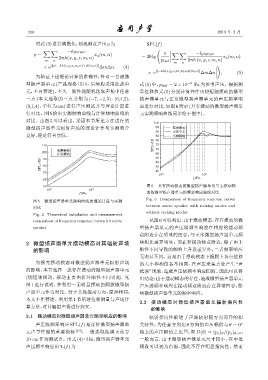
50 图 6 具有摆动模态的微型扬声器单元与无摆动模

10 2 10 3
f/Hz 态的微型扬声器单元的频率响应曲线对比
Fig. 6 Comparison of frequency response curves
图 5 微型扬声器单元频响曲线的理论计算与实测
between micro speaker with rocking modes and
对比
without rocking modes
Fig. 5 Theoretical calculation and measurement
comparison of frequency response curves for micro 从图6可以看出，由于摆动模态，存在摆动的微
speaker 型扬声器单元的声压级频率响应在相应的摆动频
点附近存在明显的凹谷，与正常微型扬声器单元频

2 微型扬声器单元摆动模态对其辐射声场 响相比差异明显。而在非摆动频点附近，除了由于
的影响 顺性不同导致的频响上升段差异外，二者频率响应
无明显不同。这是由于摆动模态下振膜上各点位移
为探究摆动模态对微型扬声器单元辐射声场 的大小和相位各不相同，在声压采集点处产生 “声
的影响，本节选择一款存在摆动的微型扬声器单元 抵消”现象，造成声压级频率响应凹陷。因此可以得
(绕短轴摆动，摆动主要由折环顺性不同引起，见 出结论：由于摆动模态的存在，造成微型扬声器单元
图 1 进行说明，并利用一无明显摆动的同款微型扬 声压级频率响应在摆动频点附近存在异常凹谷，影
声器单元作为对比。对于其他摆动方向，原理相同， 响微型扬声器单元的频率响应。
本文不作赘述。利用第 1 节所述位移测量与声场计
2.2 摆 动 模 态 对 微 型 扬 声 器 单 元 辐 射 指 向 性
算方法，对其辐射声场进行探究。
的影响
2.1 摆动模态对微型扬声器单元频率响应的影响 辐射指向性描述了声源辐射随方向而异的相
声压级频率响应 SPL(f) 是评价微型扬声器单 关特性，为任意方向角 θ 方向的声压幅值与 θ = 0 ◦
元声学性能的重要指标 [10] ，一般选取振膜正前方 轴上的声压幅值之比 [9] ，即 D(θ) = (p a ) θ /(p a ) θ=0 。
10 cm 作为测试点。由式 (4) 可知，微型扬声器单元 一般而言，由于微型扬声器单元尺寸较小，在中低
声压频率响应SPL(f)为 频段可以视为点源，因此不存在明显指向性。然而