Page 168 - 应用声学2019年第4期

628 2019 年 7 月

0 4
ඵࣱکӉ 3
5
ඵࣱ᭤کӉ RMSE 2
10 1
15 0 0 10 20 30 40 50 60 70 80
๒ງ/m 20 ᡰሏ/km

25 (a) ܦູງए10 m
30 1.5
RMSE 1.0
35
40
85 90 95 100 105 110 115 120 125 130 0.5
0 10 20 30 40 50 60 70 80
͜୧૯ܿ/dB
ᡰሏ/km
(a) ܦູງए10 m
(b) ܦູງए20 m
0 4
5 3
ඵࣱکӉ
10 ඵࣱ᭤کӉ RMSE 2
15 1 0
๒ງ/m 20 0 10 20 30 ᡰሏ/km 50 60 70 80
40
25 (c) ܦູງए35 m
30
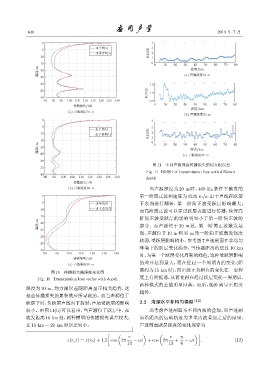
图 11 不同声源深度传播损失的均方根误差
35
Fig. 11 RMSE of transmission loss with different
40
90 95 100 105 110 115 120 125 130 depth
͜୧૯ܿ/dB
(b) ܦູງए20 m 当声源深度为 20 m 时，400 Hz 条件下激发的
0 第一阶简正波相速度为 1535 m/s，由于声线在跃层
5 ඵࣱکӉ 下表面进行翻转，第一阶简正波受跃层影响最大。
10 ඵࣱ᭤کӉ
而高阶简正波可以穿过跃层表面进行传播，使得高
15 阶简正波受跃层的影响明显小于第一阶简正波的
๒ງ/m 20 部分。而声源位于 20 m 处，第一阶简正波激发最
25
强，声源位于 10 m 和 35 m 第一阶简正波激发强度
30
较弱，受跃层影响较小。参考图7声速剖面在非均匀
35
环境下的跃层变化趋势，当传播距离约经过 10 km
40
80 90 100 110 120 130 140
时，为第一个跃层变化周期的峰值，这种受跃层影响
͜୧૯ܿ/dB
的差异达到最大，而在经过一个周期内的变化 (距
(c) ܦູງए35 m
离约为15 km时)，简正波正负相位的变化在一定程
图 10 传播损失随深度变化图
Fig. 10 Transmission loss varies with depth 度上有所抵消，从而使得在经过跃层变化一周期后，
两种模式的差值明显回落。而后，随距离呈正相关
深度为 10 m，均方根误差随距离呈正相关趋势，这
趋势。
是由传播损失的累积效应所导致的。而当声源位于
跃层下时，负跃层声线向下折射，声场受跃层的影响 2.2 海深水平非均匀模型 [15]
较小。由图 11(b) 可以看出，当声源位于跃层中，在 当考虑声速剖面为不同内波的叠加，即声速剖
收发距离 10 km 处，两种模型的传播损失误差较大， 面沿距离的运动轨迹为多重内波叠加之后的结果，
在15 km ∼ 20 km时误差较小。 声速剖面跃层深度的变化规律为

[ ( ) ( )]
r r π
z(r, t) = z(r 0 ) + 1.5 cos 2π − ωt + cos 2π + − ωt . (12)
13 13 6