Page 45 - 应用声学2019年第5期

第 38 卷 第 5 期 朱文发等： 轨道板中超声兰姆波传播的有限元计算和实验 797

在板中传播的兰姆波，若由频散曲线得到某一 表 2 二维有限元仿真模型的参数
频率下的波数k 2 ，则相速度为 c 2 =ω/k 2 。因此，当使 Table 2 Parameters of two-dimensional
用空气耦合超声探头激励时，声束的入射角 θ 可以 FE simulation model
由Snell定律 [9] 得到：
参数 值
( )
θ = arcsin c 1 , (3) 材料 轨道板
c 2
板尺寸 (长 × 高)/mm 2000 × 200
其中，c 1 为空气中的声速。
时间步长/s 7.5 × 10 −8
根据式(3)，可得到兰姆波的相速度频散曲线各
网格尺寸/mm 0.5×0.5
模态的入射角 -频厚积的频散曲线。如图 2 所示，当
吸收边界尺寸/mm 250
板厚一定时，入射声波的频率与入射角之间是一一
探头距离板表/mm 20
对应的关系，当入射角为 8.8 、激励频率为 50 kHz
◦
沿轨道板板厚和宽度中心以 20 mm为步长，采
时，轨道板中A0模态的兰姆波趋于Rayleigh波。一
集 10 个点的数据如图 4(a) 所示。根据兰姆波的波
般情况下，为保证接收到较强的兰姆波，要求接收探
包到达不同接收点的时间差，可以计算出兰姆波
头的频率与角度和激励探头相同。
的群速度为2220 m/s，与Rayleigh 波的理论群速度
30
S0 A0 2247 m/s 相吻合。在远离激励源的位置，在A、B 两
25 S1 A1
S2 A2 点间，以5 mm为步长，沿轨道板板厚和宽度中心采
20 S3 A3 集 201组数据，并对采集到数据做二维傅里叶变换。
К࠱ᝈ/(O) 15 К࠱ᝈ8.8° 如图 4(b) 所示，红线表示解析理论计算得到的 f-k
曲线，在50 kHz 的激发频率下二维傅里叶变换系数
10
5 的较大值沿Rayleigh波的频散曲线分布。有限元计
算结果与理论分析一致，频厚积较大时，A0 模态趋
0
0 6 12 18 24 30
ᮠԒሥ/(MHzSmm) 于Rayleigh波。
图 2 入射角 -频厚积的频散曲线
Fig. 2 Incident angle-f ·d dispersion curve

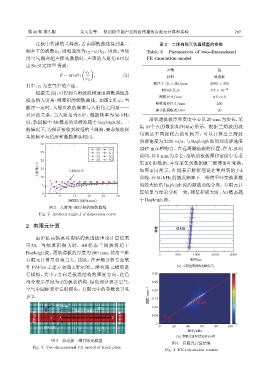
2 有限元计算
ࣨϙ ၌Ѿฉ
由沪杭高铁嘉兴南站的轨道板理论计算结果
可知，当频厚积很大时，A0 模态兰姆波将趋于
Rayleigh波。而轨道板的厚度为200 mm，使用三维
0 500 1000 1500 2000
有限元计算量将相当大。因此，在声场分析专业软 ௑ᫎ/µs
件 PZFlex 上建立如图 3 所示的二维有限元模型进 (a) ˀՏͯᎶଌஆ҂ᄊηՂ
行模拟，其中 z 方向是板状结构的厚度方向，红色 0.30 1
部分表示厚度为 d 的板状结构，绿色部分表示空气， 0.25
空气中圆柱表示发射探头。有限元中的参数设置见 0.20
表 2。 ฉ஝/mm -1 0.15

θ ԧ࠱ଊ݀ 0.10 ၌Ѿฉ
ቇඡ
С201˔ଌஆག
ծஆ᣸ႍ d A B ծஆ᣸ႍ 0.05 A0 S0

౜࿄ፇ౞ z ቇඡ 0 0 20 40 60 80 100 0
x ᮠဋ/kHz
(b) దᬍЋᝠካፇ౧ᄊf-kڏ
图 3 轨道板二维有限元模型
图 4 有限元计算结果
Fig. 3 Two-dimensional FE model of track plate
Fig. 4 FE calculation results