Page 67 - 应用声学2019年第5期

第 38 卷 第 5 期 张政等： 声表面波在圆弧处反射及透射的数值研究 819

能量不断减小。同理，截取位移波形图 3(b) 中 t 由 时，RTP的能量随着圆弧半径的增加而不断增大的，
3.5 µs 增至 4.5 µs，对透射表面波信号 (观测点均为 虽然此时反射表面波的能量在减少，但是表面波发
Re5) 进行详细分析，结果如图 5 所示。当圆弧半径 生模式转换的能量在不断增大，因此透射表面波的
小于 400 µm 时，透射表面波的能量是随着弧形曲 能量仍然在不断减小。为了进一步验证上述的结
率半径的增大而减小的，当圆弧半径大于 500 µm 论，设置对照数值实验组，将上升时间由 10 ns 增至
时，透射表面波的能量是随着弧形曲率半径的增大 100 ns，但仍然保持激光线源半宽为 100 µm。将反
而增大的。 射表面波与透射表面波的位移幅值和与其对应的
将反射表面波与透射表面波的位移幅值和与 圆弧半径大小分别绘制在图6(b)中。从图6(b)中可
其对应的圆弧半径大小分别绘制在图6(a)中。当圆 以看出，当圆弧半径r < 0.5λ时，反射表面波的能量
弧半径 r < 0.5λ (λ 代表一个表面波中心波长) 时， 是不断增大的；当r = 0.5λ时，此时反射的表面波能
反射表面波的能量是不断增大的；当r = 0.5λ时，此 量达到最大；当圆弧半径 0.5λ < r < λ 时，RTP 的
时反射的表面波能量达到最大；当 r > λ 时，反射 能量随着圆弧半径的增加而不断增大的，如图 7(b)
表面波的能量随着圆弧半径的增大不断减小，透射 所示；当圆弧半径 r > λ 时，反射表面波的能量随着
表面波的能量随着圆弧半径的增大不断增大，增长 圆弧半径的增大不断减小，透射表面波的能量随着
率逐渐减小，表明圆弧半径增大到某一数值时，表 圆弧半径的增大不断增大，两种情况所观察到的现
面波能够完全绕行，不再发生反射。但是反射表面 象是一致的。
波的能量最大值在 r = 0.5λ 处，透射表面波的能量 图 8 展示了圆弧半径分别取 0 µm、200 µm、
最小值在 r = λ 处，即当反射表面波的能量最大时， 400 µm、600 µm、800 µm和1000 µm时，表面波(此
此时透射表面波的能量并非最小。分析原因发现 时一个表面波中心波长在 430 µm 左右) 在圆弧处
是表面波在圆弧处的部分反射是伴随着模式转换 的位移图像。从图 8 中可以更加直观地看出，当圆
的，当 r < λ 时，圆弧仍然可以看作是一个奇异点。 弧半径小于一个表面波中心波长时，表面波在圆弧
如模拟圆弧半径由 200 µm 增至 1000 µm (步长值 过渡面是以反射与模式转换为主；当圆弧半径大于
为100 µm)，截取位移波形图3(a)中t由3.2 µs增至 一个中心表面波波长时，随着半径不断增大，反射回
3.6 µs，对直达表面波转化为纵波 (RTP) 信号进行 来的表面波能量不断减少，此时表面波在圆弧过渡

详细分析，如图7(a) 所示；当圆弧半径 0.5λ < r < λ 面是以透射为主。
1.0 1.0
Re2ͯረࣨϙ
0.9 0.9 લՌజጳ
Re5ͯረࣨϙ
લՌజጳ
0.8 0.8
Re2ͯረࣨϙ
લՌజጳ
0.7 Re5ͯረࣨϙ 0.7
ͯረ/nm 0.6 લՌజጳ ͯረ/nm 0.6

0.5 0.5
0.4 0.4

0.3 0.3

0 400 800 1200 1600 2000 0 400 800 1200 1600 2000
ړऻӧय़/µm ړऻӧय़/µm
(a) ༏АູʽӤ௑ᫎ t 0 =10 ns (b) ༏АູʽӤ௑ᫎ t 0 =100 ns
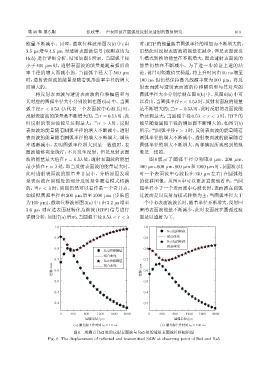
图 6 观测点 Re2 处的反射表面波与 Re5 处的透射表面波位移幅值图
Fig. 6 The displacement of reflected and transmitted SAW at observing point of Re2 and Re5