Page 66 - 应用声学2019年第5期

818 2019 年 9 月

刻；同时，入射超声波到达边缘时，根据惠更斯原理， 圆弧过渡面处发生反射及透射的过程。模拟圆弧半
拐点相当于一个次声源 [16] 会重新产生纵波和表面 径由 0 µm 增至 2000 µm(步长值为 100 µm)，截取
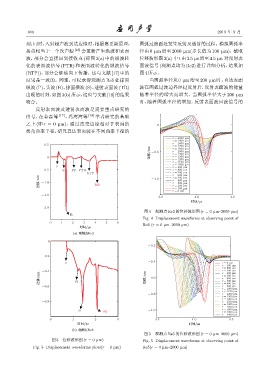
波，部分会直接回到接收点 (即图 3(a) 中的纵波转 位移波形图3(a) 中t由3.5 µs增至4.5 µs，对反射表
化的表面波信号 (PTR) 和表面波转化的纵波信号 面波信号 (观测点均为 Re2) 进行详细分析，结果如
(RTP))，部分会继续向下传播。这与文献 [17] 中的 图 4所示。
结果是一致的。同理，可以求得观测点 Re5 处掠面 当圆弧半径从 0 µm 增至 200 µm 时，直达表面
纵波 (P)、头波 (H)、掠面横波 (S)、透射表面波 (TR) 波在圆弧过渡边界经过反射后，反射表面波的能量
出现的时刻，如图3(b)所示，这也与文献[18]的结果 随着半径的增大而增大。当圆弧半径大于 200 µm
吻合。 时，随着圆弧半径的增加，反射表面波回波信号的
反射表面波及透射表面波是需要重点研究的

信号，在金磊等 [17] 、冯湾湾等 [18] 学者研究的基础
之上 (即 r = 0 µm)，通过改变边缘相对于表面的 0
拐角曲率半径，研究直达表面波在不同曲率半径的
r=2000 µm
r=1900 µm
0.5 r=1800 µm
r=1700 µm
ͯረ/nm -0.5 r=1500 µm
r=1600 µm
r=1400 µm
0 r=1300 µm
r=1200 µm
r=1100 µm
r=1000 µm
P r=900 µm
-0.5 S PP PTR r=800 µm
RTP r=700 µm
r=600 µm
ͯረ/nm -1.0 RR -1.0 r=500 µm
r=400 µm
r=300 µm
r=200 µm
r=100 µm
r=0 µm
-1.5
3.5 4.0 4.5
௑ᫎ/µs
-2.0
图 4 观测点 Re2 的位移波形图 (r = 0 µm–2000 µm)
R
Fig. 4 Displacement waveforms at observing point of

0 1 2 3 4 5 6 Re2 (r = 0 µm–2000 µm)
௑ᫎ/µs
(a) ᜺฾གRe2

0
-0.2
-0.2
-0.4
P r=0 µm
r=100 µm
r=200 µm
-0.4 r=300 µm
r=400 µm
ͯረ/nm H ͯረ/nm -0.6 r=500 µm
r=600 µm
r=700 µm
r=900 µm
-0.6 r=800 µm
r=1000 µm
r=1100 µm
-0.8 r=1200 µm
r=1300 µm
r=1400 µm
-0.8 r=1500 µm
r=1600 µm
r=1700 µm
S TR -1.0 r=1800 µm
r=1900 µm
r=2000 µm

0 1 2 3 3.5 4.0 4.5
௑ᫎ/µs ௑ᫎ/µs
(b) ᜺฾གRe5
图 5 观测点 Re5 的位移波形图 (r = 0 µm–2000 µm)
图 3 位移波形图 (r = 0 µm) Fig. 5 Displacement waveforms at observing point of
Fig. 3 Displacement waveforms plots(r = 0 µm) Re5(r = 0 µm–2000 µm)