Page 99 - 《应用声学》2019年第6期

第 38 卷 第 6 期 马立康等： 超声空化现象影响因素的实验研究 1001

(如图 2(b) 和图 2(c) 所示)。实验是在开放的环境 排水系统可以保证容器内液体缓慢流出，对实验现
中进行，在频谱图中，100∼800 Hz 频率范围的声 象影响很小，因此可以忽略排水系统对实验的影响。
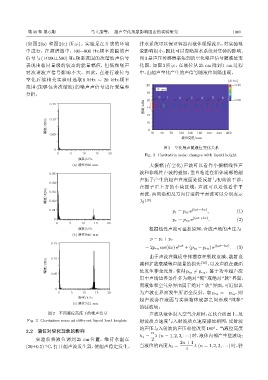
信号与 (14000±500) Hz 频率范围的次谐波声信号 图3 是声压传感器采集到的空化噪声信号随液位变
表现出相同量级的较高的能量幅值，但低频噪声 化图，如图 3 所示，在液位从 25 cm 降到 1 cm 过程
对次谐波声信号影响不大。因此，在进行液位与 中，由超声空化产生的声信号随液位间隔出现。
空化后续相关实验时选取 8 kHz ∼ 20 kHz 频率 (dBm)
范围 (能够包含次谐波) 的噪声声信号进行采集和 20 -0.25
15 mm
分析。 18
0 1 2 3 4 5 6 -0.00
16
ᮠဋ/kHz 14
0.15

12
0.10
ࣨए/dBm 10 8

0.05 10 40 70 100 130 160 190 220 250
๯ͯᰴए/mm
图 3 空化噪声随液位变化关系
0
0 5 10 15 20
Fig. 3 Cavitation noise changes with liquid height
ᮠဋ/kHz
(a) ๯ͯ˞20 mm 大振幅 (有空化) 声波可以看作小振幅线性声

0.05 波和非线性声波的叠加，垂直粘连在箱体底部的超
声振子产生的超声在液面处经反射与初始波干涉。
0.04
在振子正上方的小块区域，声波可以近似看作平
ࣨए/dBm 0.03 面波，两列沿相反方向行进的平面波可以分别表示

为
[19]
0.02
0.01 p i = p ia e j(ωt−kx) , (1)
0 p r = p ra e j(ωt+kx) . (2)
0 5 10 15 20
ᮠဋ/kHz 根据线性声波可叠加原理，合成声场的声压为
(b) ๯ͯ˞40 mm
p = p i + p r
0.15
= 2p ra cos(kx) e jωt + (p ia − p ra ) e j(ωt−kx) . (3)
由于声波在媒质中传播存在吸收衰减、散射衰
0.10
ࣨए/dBm 减和扩散衰减等声能量的损失 [20] ，以及声波在液面

0.05 处发生非全反射，使得 p ia ̸= p ra 。鉴于功率超声应
用中声场边界条件多为绝对 “硬” 或绝对 “软” 界面，
而液体和空气分界面属于绝对“ 软”界面，可近似认
0
0 5 10 15 20 为声波在界面发生所谓全反射。取 p ra = −p ia ，则
ᮠဋ/kHz
超声波会在液面与实验箱体底部之间形成 “纯粹”
(c) ๯ͯ˞12 mm
的驻波场。
图 2 不同液位高度下的噪声信号 声波从液体射入空气介质时，在软介质面上，反
Fig. 2 Cavitation noise at different liquid level heights 射波质点速度与入射波质点速度相位相同，反射波
的声压与入射波的声压相位改变180 。当液位高度
◦
2.2 液位对空化现象的影响 n
h 1 = λ (n = 1, 2, 3, · · · )时，液体内部产生驻波场；
实验前将液位调到 25 cm 位置，维持水温在 2
2n + 1
(20±0.5) C，打开超声波发生器，使超声稳定发生。 当液位的高度h 2 = λ (n = 1, 2, 3, · · · )时，驻
◦
4