Page 47 - 《应用声学》2020年第1期

第 39 卷 第 1 期 金宁德等： 油 -气 -水三相流超声传感器持气率测量 43

利用公式 (12) 可计算得到不同流体工况下的 0.9 +20%
瞬态气泡弦长序列。然后，再用一维概率密度函数 0.8
对弦长序列进行拟合，便可得到泡状流中气泡泡径 0.7
的概率密度分布曲线。 0.6

图 13 显示了泡状流中的液相表观流速 U sl = Y gs
0.5 AAD=0.0442
1.1776 m/s 时，不同气相表观流速时气泡泡径概率 AAPD=0.0928
0.4
密度分布曲线。从图中可以看出，对于同一种气相
0.3 Y gs =1.13294Y gqcv -0.02225
流速 U sg 而言，概率密度峰值对应的气泡泡径 D 相 R =0.97079
2
0.2
差不多，但随着气相流量的不断增加，概率密度峰值 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
Y gqcv
对应的气泡泡径 D 值也在逐渐变大，但是概率密度
(a) ඀܋ื
峰值在逐渐减小。说明持气率的增加使得气泡泡径
0.6
变大，但气泡间的泡径差异逐渐变大，而在持气率预 +22%
测模型中，气泡泡径被假设为单一值。气泡泡径的
0.5
非均分布导致利用超声脉冲衰减预测的持气率偏
离混合流体中的真实持气率。 Y gc
0.4 AAD=0.0536
3.3 段塞流与混状流测量及分析 AAPD=0.1380
对段塞流与混状流而言，当气塞经过超声传感
0.3 Y gc =1.2151Y gqcv -0.02914
器时，传感器输出截止的低电平，而段塞流的液塞中 R =0.92087
2
分布有分散的气泡，与泡状流相似。故对段塞流的 0.3 0.4 0.5 0.6
Y gqcv
液塞部分可以使用式 (7) 计算它的持气率，再通过 (b) ຉ࿄ื
计算气塞与液塞所占的比例，即可求出段塞流的持
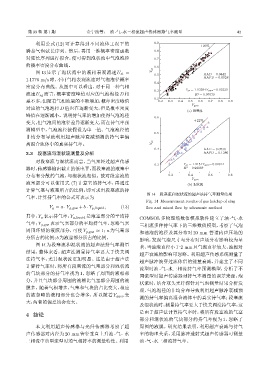
图 14 段塞流和混状流的超声法持气率测量结果
气率，计算持气率的公式可表示为
Fig. 14 Measurement results of gas holdup of slug
Y g = a · Y g,gas + b · Y g,liquid , (13) flow and mixed flow by ultrasonic method
其中，Y g 表示持气率；Y g,liquid 是液塞部分的平均持
COMSOL 多物理场数值模拟软件建立了油 -气 -水
气率；Y g,gas 表示气塞部分的平均持气率，忽略气塞
三相流多种持气率下的三维数值模型，考察了气泡
周围环绕的液膜部分，可使 Y g,gas ≈ 1；a 为气塞部
和油泡的泡径及其分布对 20 mm 管道内声压场的
分所占的比例；b为液塞部分所占的比例。
影响，发现气泡尺寸与分布对声场分布影响较为显
图 14 为段塞流和混状流的超声法持气率测量
著，当油泡直径小于 2 mm 且气泡直径较大，油相对
结果，整体来看，超声法测量持气率要大于快关阀
超声衰减的影响可忽略。利用超声传感系统测量了
法持气率，尤其混状流更加明显。这是由于超声法
超声脉冲波穿过流体后的能量衰减，并建立了不同
计算持气率时，将所有段塞流的气塞部分和混状流
流型时油 -气 -水三相流持气率预测模型，分析了不
的气块部分的持气率视为 1，忽略了周围的液相部
同流型时超声传感器对持气率测量的误差来源：泡
分，并且气块部分周围的液相比气塞部分周围的液
状流时，结合双头光纤探针对气泡测量结果分析发
膜多。随着气相增多，气塞和气块的占比变大，相应
现，气泡泡径的非均分布导致利用超声脉冲衰减预
的被忽略的液相部分也会增多，所以随着 Y gqcv 变
测的持气率偏离混合流体中的真实持气率；段塞流
大，两者的偏差均会变大。
及混状流时，测量持气率要大于快关阀法持气率，这
是由于超声法计算持气率时，将所有段塞流的气塞
4 结论
部分和混状流的气块部分的持气率视为 1，忽略了
本文利用超声传感器与光纤传感器考察了超 周围的液膜。研究结果表明，利用超声衰减与持气
声传感器对内径为 20 mm 管径垂直上升油 -气 - 水 率的物理关系，采用脉冲透射式超声传感器可测量
三相流中典型流型时的气相持率的测量特性。利用 油-气-水三相流持气率。