Page 45 - 《应用声学》2020年第1期

第 39 卷 第 1 期 金宁德等： 油 -气 -水三相流超声传感器持气率测量 41

截面积 a 与持气率 Y g 及 Sauter 平均气泡直径之间 ⇁̺
⊲
有如下关系：
6Y g
a = . (6) ֓̺
⊲
d sm
故公式 (5) 可转换为超声衰减与持气率之间的函数 Y gb
关系，即 ⊲
AAD=0.0195
( ) ( )
U 3n AAPD=0.0820
− ln = Y g L, (7)
U 0 8θ ⊲
⊲ ⊲ ⊲ ⊲
其中，散射系数 θ 为定值，由气相与液相的性质、管 Y gqcv
道材料以及实验设备共同决定，可从实验中获得。
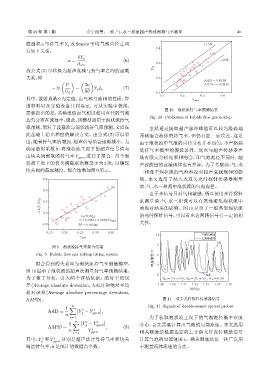
图 10 泡状流持气率预测结果
需要指出的是，该模型假定气相以相同直径的气泡
Fig. 10 Prediction of bubble flow gas holdup
均匀分布在流体中，因此，该模型适用于泡状流持气
率预测，而对于段塞流与混状流持气率预测，文后在 虽然通过提取超声脉冲峰值可以较为准确地
此基础上给出相应的解决方案。由公式 (7) 可以看 预测混合流体的持气率，但仍存在一定误差，这是
出，随着持气率的增加，超声信号值会逐渐减小。为 由于泡状流中气泡的直径分布并不均匀，不严格满
确定散射系数 θ，将泡状流工况下的超声信号值与 足持气率模型的假设条件。这也与超声传感器声
由快关阀截取的持气率 Y gqcv 进行了拟合。每个泡 场有限元分析结果相吻合，即气泡泡径不同时，超
状流工况下的快关阀截取次数至少为 3 次，以确保 声波能量的衰减规律也有差异。为了考察油-气-水
快关阀的截取精度。拟合结果如图9所示。 三相流中泡状流的气泡泡径对超声衰减规律的影

2.8 响，本文选用了插入式双头光纤探针传感器测量
油-气-水三相流中泡状流的气泡泡径。
2.6
由于光信号只对气相敏感，所以使用光纤探针
-ln↼U⊳U 0 ↽ 2.4 来测量油 -气 -水三相流可以有效地避免泡状流中
油泡对结果的影响。图 11 显示了一组典型泡状流
2.2
-ln(U⊳U 0) 的光纤探针信号，可以看出这两路信号有一定的相
=1.54984+3.06593Y gqcv
2.0 R =0.80346 关性。
2
0.15 0.20 0.25 0.30 0.35
 ʾ຤͜ਖ٨
Y gqcv
ʽ຤͜ਖ٨
ඡจ

图 9 泡状流持气率拟合结果
ႃԍηՂ/V
Fig. 9 Bubble flow gas holdup fitting results 
拟合得到的关系即为泡状流持气率测量模型， 
图 10显示了泡状流的超声法测量持气率预测结果。
 ๯ᄱ
为了便于分析，引入两个评估依据：绝对平均误 Q g /⊲ m /d֒ Q l / m /d֒ K w /⊲
3
3
差 (Average absolute deviation, AAD) 和绝对平均 ⊲ ⊲ ⊲ ⊲ ⊲ ⊲ ⊲
௑ᫎ/s
相对误差 (Average absolute percentage deviation,
AAPD)。 图 11 双头光纤探针传感器信号
n Fig. 11 Signals of double-sensor optical probes
1 ∑ i i
AAD = Y − Y gqcv ,
g
n
i=1 为了获取泡状流工况下的气泡泡径概率密度
n i i
1 ∑ Y − Y gqcv 分布，首先需要计算出气泡的局部流速。本文选用
g
AAPD = , (8)
i
n Y gqcv 相关测速法根据选定的上下游光纤探针测量信号
i=1
i
其中，Y 和 Y i 分别是超声法计算持气率和快关 计算气泡的局部速度 v。相关测速法是一种广泛用
g gqcv
阀法持气率，n是统计的数据点个数。 于测量流体流速的方法。