Page 62 - 《应用声学》2020年第3期

382 2020 年 5 月

型中钢层厚度为 19 mm，混凝土层厚度为 250 mm。 的频散曲线，如图 4 所示，选取入射角度为 4.9 ，接
◦
为了消除边界反射的干扰，在有限元模型中加入吸 收点数 64，接收点距离 3 mm。由于板状结构中同
收边界，有限元仿真参数如表2所示。 时存在多个模态的 Lamb 波，需要通过二维傅立叶

变换将幅度 -时间曲线转换成频率 -波数 (f-k) 关系
༏ԧnjଌஆଊ݀ ቇඡ
С64˔ଌஆག 图，各个模态可以根据 (频率，波数，幅值) 的关系分
ծ ծ
ஆ ᨂ ஆ 离并进一步得到确认，这样就可以进行频散曲线的
᣸ ᣸
ႍ ႍ 定量测量 [11] 。为了更加清楚地观察到导波在钢 -混
ຉіژ 凝土界面层中传播的各个模态，将有限元结果进行
二维傅里叶变换，结果如图5所示。
图 3 有限元仿真模型
30
Fig. 3 Finite element simulation model
S0
25 A0
表 2 有限元仿真模型参数 S1
20 A1
Table 2 Finite element simulation model
ᝈए/(°)
parameters 15
单元 吸收边界 探头距离 10 (125 kHz, 4.9°)
材料 板尺寸/mm 时间步长/s
尺寸/mm 尺寸/mm 板表/mm
5
钢板 600×500×19 7.5×10 −5 0.11 150 5
0
0 100 200 300 400 500
2.2 厚度为2 mm界面层的数据分析 ᮠဋ/kHz
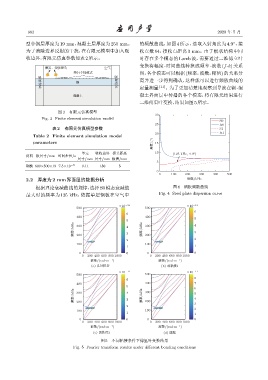
根据理论衰减曲线的规律，选择S0模态衰减值 图 4 钢板频散曲线
最大时的频率为 125 kHz，依据单层钢板在空气中 Fig. 4 Steel plate dispersion curve

T10 -11 T10 -11
500 500
6
6
400 400 5
5
ᮠဋ/kHz 300 4 3 ᮠဋ/kHz 300 4 3
200
2 200 2
100 100
1 1
0 0 0 0
0 200 400 600 800 1000 0 200 400 600 800 1000
ฉ஝/(radSm -1 ) ฉ஝/(radSm -1 )
(a) ᓢݞዥଌ (b) ीዥଌ1
T10 -11 T10 -11
500 500
8
6
400 400 7
5 6
ᮠဋ/kHz 300 4 3 ᮠဋ/kHz 300 5 4
200
200
3
2
2
100 100
1
1
0 0 0 0
0 200 400 600 800 1000 0 200 400 600 800 1000
ฉ஝/(radSm -1 ) ฉ஝/(radSm -1 )
(c) ीዥଌ2 (d) ᑲዥ
图 5 不同粘接条件下傅里叶变换结果
Fig. 5 Fourier transform results under different bonding conditions