Page 77 - 《应用声学》2020年第3期

第 39 卷 第 3 期 周烨等： 基于听觉特性的舰船辐射噪声信号仿真 397

40
3 调制谱模拟
30
在构建调制谱时，其模型主要表示为 [6]
20 [ ∑ ]
Ҫဋ៨/dB 10 S m (t) = 1 + i B i sin(i · 2πf z t) · n(t), (4)

0
其中，n(t)表示被调制信号，B i 表示调制幅度，f z 表
示舰艇轴频。由于调制谱来源于螺旋桨空化引发的
-10
调制效应，文献[10]中将空化气泡群看成组结构、随
-20
0 200 400 600 800 1000 机形状与幅度的信号包络模型。在接收点，将 N 叶
f/Hz
螺旋桨空化噪声功率看成各叶片空化声功率的叠
图 1 提取连续谱噪声
加，经过计算包络谱线谱族数学期望值从而得到了
Fig. 1 Extracting continuous spectrum noise
信号包络前八阶谐波族特征所体现的结构特性，针
对不同螺旋桨叶数研究了不同谐波幅值关系。
25
对于三叶桨，有
20
b(3) > b(n), n ∈ [4, 8],
Ҫဋ៨/dB 15 b(1) > b(2) > b(4) > b(5) > b(7) > b(8). (5)
四叶桨：
10

b(4) > b(n), n ∈ [5, 8],
5
b(1) > b(3) > b(5) > b(7),
0
0 200 400 600 800 1000 b(2) > b(6). (6)
f/Hz
五叶桨：
图 2 平滑处理
Fig. 2 Smoothing b(5) > b(n), n ∈ [6, 8],
b(2) > b(3) > b(7) > b(8),
1.0
b(1) > b(4) > b(6). (7)
0.8
六叶桨：
ॆʷӑࣨए 0.6 b(6) > b(n), n ∈ [7, 8],
b(1) > b(5) > b(7),
0.4
b(2) > b(4) > b(8). (8)
0.2
七叶桨：
0
0 0.2 0.4 0.6 0.8 1.0 b(1) > b(6) > b(8), b(2) > b(5),
ॆʷӑᮠဋ
b(3) > b(4), b(7) > b(8). (9)
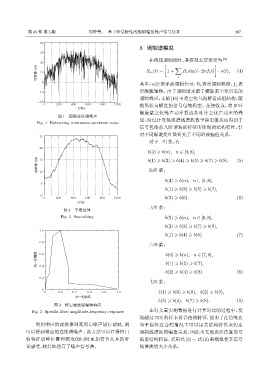
图 3 特定滤波器幅频响应
Fig. 3 Specific filter amplitude-frequency response 在对大量实测数据进行计算对比的过程中，发
现超过 75% 的样本符合结构特征，说明了在信噪比
利用响应的滤波器对高斯白噪声进行滤波，就 与平稳性适合的情况下可以用其结构特性来约束
可以得到相应的连续谱噪声。此方法可以在保持目 调制线谱族的幅值关系，因此本文假设所仿真信号
标特征谱峰位置和幅度的同时更加符合人耳的听 满足结构特征，采用式 (5) ∼ 式(9) 来模拟仿真信号
觉感受，较好地仿真了噪声信号谱。 线谱族的大小关系。