Page 79 - 《应用声学》2020年第3期

第 39 卷 第 3 期 周烨等： 基于听觉特性的舰船辐射噪声信号仿真 399

(2) 设定搜索次数 N，通过在约束条件下产生 频率按照式 (5) ∼ 式 (9) 的结构关系设置幅值代入
N 个辐射噪声仿真信号，表示为 式 (15)，仿真得到一系列辐射噪声。计算其各自分
[ ]
∑ 段谱质心值，通过固定搜索次数下的数据对比输出
S N (t) = 1 + B iN sin(i · 2πf z t)
最优解，如图6、图7所示。
i
× [Y c (t) + L N (t)], (15)
表 1 线谱及调制谱频率
其中，Y c (t)表示按照样本连续谱特征生成的仿真连
Table 1 Line spectrum and modulation
续谱信号，S N (t)表示单次搜索次数下的仿真信号。 spectrum frequency

(3) 计算仿真信号的分段谱质心 Q N (l), l =
1, · · · , L。 频谱类型 频率分布/Hz
(4) 将仿真值带入模型求解，搜索匹配结果。 机械噪声线谱 57、114、228、456、912
(5) 在N 个匹配结果中提取最小值作为最优匹
螺旋桨噪声线谱 68、136
配结果，当存在多个最优结果时，取频带谱质心方差
调制线谱 16.7、33.4、66.8、133.6、267.2、534.4
最小信号输出。

6 算例仿真 1000
500
ࣨϙ
通过采集的某四叶桨商船以 15 kn 航速匀速航
0
行时的辐射噪声，采样率为5 kHz，进行分段谱质心
-500
计算，考虑到计算效率，本文仿真时采用 6 段分频， 0 1000 2000 3000 4000 5000
᧔ನག
可以在保证区分度的情况下提高计算效率，结果如 (a) ᣣ࠱٪ܦ௑۫ฉॎ
图5所示。 0.5

2500
ࣨϙ 0

2000 -0.5 0 1000 2000 3000 4000 5000
О඀៨᠏ॷ/Hz 1500 (b) ଌஆηՂ௑۫ฉॎ
᧔ನག

1000
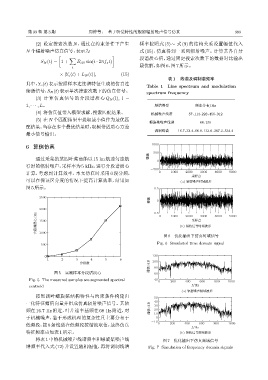
图 6 优化输出下仿真时域信号
Fig. 6 Simulated time domain signal
500

0 120
1 2 3 4 5 6
៨ጟ/dB 80
Ѭ඀஝ 100
图 5 实测样本分段谱质心 60
Fig. 5 The measured samples are segmented spectral 40 0 200 400 600 800 1000
centroid f/Hz
(a) ᣣ࠱٪ܦᮠ۫ฉॎ
按照四叶螺旋桨结构特性与约束条件构建归 50
一化特征幅值向量并组成仿真辐射噪声信号。其轴 40
30
频在 16.7 Hz 附近，叶片速率基频在 68 Hz 附近，对 ៨ጟ/dB 20
10
于机械噪声，鉴于形成机理的复杂性且主要分布于 0
-10
低频段，按8 条线谱在低频段按谐波取值，最终仿真 0 200 400 600 800 1000
f/Hz
特征频率点如表1所示。 (b) ଌஆηՂᮠ۫ฉॎ
将表 1中的机械噪声线谱频率和螺旋桨噪声线 图 7 优化输出下仿真频域信号
谱频率代入式 (12) 并设置随机幅值，再将调制线谱 Fig. 7 Simulation of frequency domain signals