Page 24 - 《应用声学》2020年第5期

666 2020 年 9 月

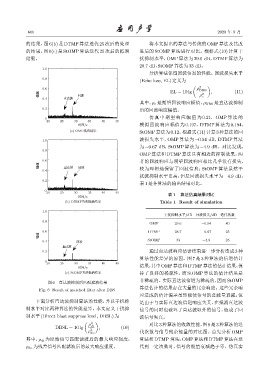
的结果，图 6(b) 是 DTMP 算法迭代 25 次后的处理 将本文提出的算法与传统的 OMP 算法及其改
的结果，图 6(c) 是 StOMP 算法迭代 25 次后的抵消 进后的 StOMP 算法进行对比。根据式 (10) 计算干
结果。 扰抑制水平，OMP 算法为 29.6 dB，DTMP 算法为
28.7 dB，StOMP算法为33 dB。
1.0
分析算法保留回波信息的性能。回波损失水平
0.8
(Echo loss, EL)定义为
( 2 )
0.6 EL = 10 lg ρ DBS (11)
ࣨϙ ڀฉ ρ 2 e ,
0.4 ᄰ᣺ฉ
其中，ρ e 是期望回波响应幅值，ρ DBS 是直达波抑制
0.2 后的回波响应幅值。
仿真中期望响应幅值为 0.21，OMP 算法的
0
20 25 30 35 40 45
௑ᫎ/s 模拟回波响应幅值为 0.197，DTMP 算法为 0.194，
(a) OMPખ๗ፇ౧ StOMP算法为0.12。根据式 (11)计算3种算法的回
波损失水平，OMP 算法为 −0.54 dB，DTMP 算法
1.0
为 −0.67 dB，StOMP 算法为 −4.9 dB。对比发现，
0.8
OMP 算法和 DTMP 算法具有相近的抑制效果，两
0.6 者的回波响应与期望回波响应相比几乎没有损失，
ࣨϙ ᄰ᣺ฉ ڀฉ 较为理想地保留了回波信息；StOMP 算法虽然干
0.4
扰波抑制水平更高，但是回波损失水平为 −4.9 dB。
0.2
表 1是各算法的输出结果对比。
0
20 25 30 35 40 45 算法仿真结果对比
௑ᫎ/s 表 1
(b) DTMPካขખ๗ፇ౧ Table 1 Result of simulation

1.0
干扰抑制水平/dB 回波损失/dB 迭代次数
0.8
OMP 29.6 −0.54 80
0.6 DTMP 28.7 −0.67 25
ࣨϙ
0.4 ڀฉ StOMP 33 −4.9 25
ᄰ᣺ฉ
0.2 通过直达波响应估计结果进一步分析造成3 种
算法性能差异的原因。图 7 是 3 种算法的信道估计
0
20 25 30 35 40 45 结果，其中OMP算法和DTMP算法的估计结果，保
௑ᫎ/s
(c) StOMPካขખ๗ፇ౧ 持了良好的稀疏性，而 StOMP 算法的估计结果是
非稀疏的。实际直达波信道为稀疏的，因而 StOMP
图 6 直达波抑制后匹配滤波结果
算法估计的结果存在大量的冗余响应。这些冗余响
Fig. 6 Result of matched filter after DBS
应造成的估计偏差虽然能使信号的总能量衰减，但
下面分析直达波抑制算法的性能，并以干扰抑 是由于与实际直达波信道响应失真，在抵消直达波
制水平对比两种算法的性能差异。本文定义干扰抑 信号的同时也破环了直达波以外的信号，造成了回
制水平(Direct blast suppress level, DBSL)为 波信号失真。
( 2 )
ρ 对比3种算法的收敛性能，图8是3种算法的迭
DBSL = 10 lg di , (10)
ρ 2 do 代次数与信号残余能量的对比图。首先分析 OMP
其中，ρ di 为原始信号匹配滤波后的最大响应强度， 算法和DTMP 算法，OMP算法和DTMP算法在迭
ρ do 为残差信号匹配滤波后的最大响应强度。 代到一定次数时，信号的能量衰减趋于零。仿真实