Page 64 - 《应用声学》2020年第5期

706 2020 年 9 月

0 模到达时间及脉冲宽度有所差异，但差异量很小，相
邻两阶简正模的到达时间差在10 −2 秒级以下，由于
20 H 为时间相对量，受小范围变化的距离影响也非常
ܦູງए/m 40 小，因此较小的声源距离失配对于判别阈值影响很

小，方法对于声源距离失配具有较好的鲁棒性。

60 0
10
0.08 0.10 0.12 0.14 0.16
H/s 20
ܦູງए/m R=5 km
(a) ᠇೙एඵ஡ 30 R=6 km
0 40 R=4 km
50
20 60
ܦູງए/m 40 70 0.02 0.04 0.06 0.08 0.10 0.12 0.14 0.16

H/s
图 15 声源距离小范围变化时，H 值随声源深度变
60
化情况
Fig. 15 Variation of H versus source depths due
0.10 0.12 0.14 0.16 0.18 0.20
H/s to the mismatch of source range
(b) ພᡤࡏඵ஡
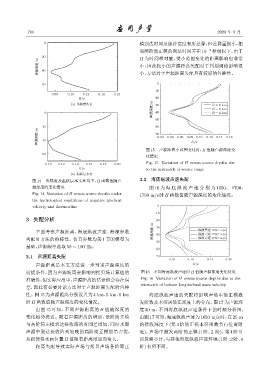
图 14 负梯度及温跃层水文环境下，H 函数值随声 3.2 海底纵波声速失配
源深度的变化情况 图 16 为 海 底 纵 波 声 速 分 别 为 1650、 1700、
Fig. 14 Variation of H versus source depths under 1750 m/s时H 函数值随声源深度的变化情况。
the hydrological conditions of negative gradient
velocity and thermocline 0
10
3 失配分析 20

下面考察声源距离、海底纵波声速、海深参数 ܦູງए/m 30 ጫฉܦᤴ1650 m/s
ጫฉܦᤴ1700 m/s
40
失配时方法的鲁棒性。仿真参数均第 1 节的模型为 ጫฉܦᤴ1750 m/s
50
基础，声源频率选取50 ∼ 100 Hz。
60
3.1 声源距离失配 70
0.05 0.10 0.15 0.20
声源距离是本文方法进一步判别声源深度的 H/s
前提条件，因为声源距离会影响到拷贝场计算值的 图 16 不同海底纵波声速时 H 值随声源深度变化情况
准确性，但实际应用中，声源距离的估计值会存在误 Fig. 16 Variation of H versus source depths due to the
mismatch of bottom longitudinal wave velocity
差，因此有必要讨论方法对于声源距离失配的鲁棒
性。图15为声源距离分别设置为 4 km、5 km、6 km 海底纵波声速的失配将影响声场中简正模激
时H 函数值随声源深度的变化情况。 发阶数及本征函数在深度上的分布。图17为声源深
由图 15 可知，不同声源距离的 H 值随深度的 度 30 m、不同海底纵波声速条件下的时频分析图，
变化趋势接近。随着声源距离的增加，低阶简正模 由图17可知，海底纵波声速为1650 m/s时，在25 m
与高阶简正模到达接收阵的时间差增加，同时水面 的接收深度下 (第 3 阶简正模本征函数节点位置附
声源中到达接收阵列较晚的高阶简正模能量占优， 近)，声场中激发两阶简正模 (1 阶、2 阶)，第 4 阶可
从而使得水面位置H 值随着距离增加而变大。 以忽略不计，与其他海底纵波声速环境(1阶、2阶、4
距离失配导致实际声场与拷贝声场各阶简正 阶)有所不同。