Page 61 - 《应用声学》2020年第5期

第 39 卷 第 5 期 于梦枭等： 能量加权时间特征用于浅海声源深度类型判别 703

3.8 由图 6 可知，不同的声源距离对应于不同的 H
3.7 曲线，阈值也有所不同。距离变远时，脉冲宽度增加，
t e =3.69 s
3.6 各阶简正模到达时间差异变大，且相比于低阶简正
௑ᫎ/s 3.5 模，高阶简正模的能量衰减要大，因而阈值变大。可
见，式(14) 中 Q 值的选取应根据声源距离的变化而
3.4
t 1 =3.33 s
改变，例如，图 6 中 5 km、10 km 和 20 km 时的阈值
3.3
分别为0.09627 s、0.1712 s、0.2339 s。当给定了声源
3.2 距离所对应的合适的 Q 值，即可实现声源深度类型
1.00 1.05 1.10 1.15 1.20 1.25 1.30 1.35 1.40
判别。
1/sin θ
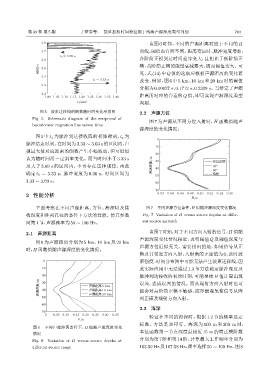
图 5 波束迁移线的倒数随时间变化示意图 2.2 声源方位
Fig. 5 Schematic diagram of the reciprocal of
图 7 为声源从不同方位入射时，H 函数值随声
beamformer migration line versus time
源深度的变化情况。
图 5 中 t 1 为脉冲到达接收阵的初始时刻，t e 为
0
脉冲结束时刻。在时间为3.33 ∼ 3.69 s的区间内，声
10
强最大值对应波束的倒数产生小幅波动，但可近似
20
认为随时间沿一定斜率变化。而当时间小于 3.33 s 30 ଌᤃ൤ഷ
及大于 3.69 s 的区间内，不再存在这种规律，由此 ܦູງए/m 40 30°
确定 t 1 = 3.33 s，脉冲宽度为 0.36 s，时间区间为 60°
ቫ࠱
50
3.33 ∼ 3.69 s。
60
70
2 性能分析 0.02 0.04 0.06 0.08 0.10 0.12 0.14 0.16
H/s

下面考察在不同声源距离、方位、海深以及接 图 7 不同声源方位条件，H 值随声源深度变化情况
收深度和阵列孔径的条件下方法的性能。仿真参数 Fig. 7 Variation of H versus source depths at differ-
同第1节，声源频率为50 ∼ 100 Hz。 ent source azimuth

2.1 声源距离 由图7可知，对于不同方向入射的信号，H 值随
声源深度变化情况接近，表明阈值 Q 及阈值深度与
图 6 为声源距离分别为 5 km、10 km 及 20 km
声源方位近似无关。需要指出的是，如果信号从正
时，H 函数值随声源深度的变化情况。
横及其邻近方向入射，入射角的正弦值为 0，此时波
0 束强度-时间分布图中可能无法产生波束迁移线，因
10 此实际应用中无法通过 1.3 节方法确定脉冲宽度及
20 脉冲到达接收阵初始时刻，可能导致 H 值计算出现
ܦູງए/m 30 ܦູᡰሏ 5 km 误差，造成误判的情况。而从端射方向入射时也可

能会对高阶简正模不敏感，应尽量避免使信号从阵
40
ܦູᡰሏ 10 km
50 ܦູᡰሏ 20 km
列正横及端射方向入射。
60
2.3 海深
70
0 0.05 0.10 0.15 0.20 0.25 0.30 0.35
验证在不同的海深时，根据 1.2 节的频率选定
H/s
标准，方法是否可行。海深为 100 m 和 200 m 时，
图 6 不同声源距离条件下，H 值随声源深度变化
本征函数第一节点深度最接近 15 m 的简正模阶数
情况
Fig. 6 Variation of H versus source depths at 分别为第 7 阶和第 14 阶，计算最大工作频率分别为
different source range 103.59 Hz及107.58 Hz，频率选择50 ∼ 100 Hz。图 8