Page 63 - 《应用声学》2020年第5期

第 39 卷 第 5 期 于梦枭等： 能量加权时间特征用于浅海声源深度类型判别 705

断的准确性，有利于获得较好的声源深度类型判别 0
性能。这也解释了 2.3 节中海深为 200 m、接收深度 10
为25 m时，出现了误判深度区间的原因。 20
ܦູງए/m 40
2.5 阵列孔径 30 ᫼Ћ஝32˔
不改变阵元间距，图11为 32 个阵元，即阵列孔 ᫼Ћ஝64˔
50
径为217 m时，声源深度为5 m及40 m 时的波束强
60
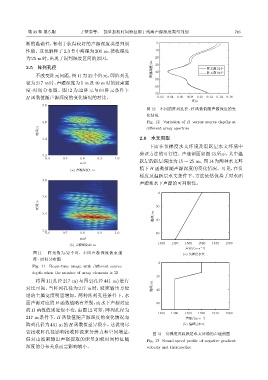
度 -时间分布图。图 12 为 32 阵元与 64 阵元条件下
70
H 函数值随声源深度的变化情况的对比。 0.02 0.04 0.06 0.08 0.10 0.12 0.14 0.16
H/s
3.8
图 12 不同的阵列孔径，H 函数值随声源深度的变
化情况

3.6 Fig. 12 Variation of H versus source depths at
௑ᫎ/s different array aperture

3.4 2.6 水文类型
下面在负梯度水文环境及温跃层水文环境中
验证方法的可行性。声速剖面如图 13所示，其中温
3.2
0.6 0.7 0.8 0.9 1.0
跃层的跃层深度为 15 ∼ 25 m。图14为两种水文环
sinθ
境下 H 函数值随声源深度的变化情况。可见，在负
(a) ܦູງए5 m
梯度及温跃层水文条件下，方法依然保持了对水面
3.8
声源和水下声源的可判别性。
0
3.6
௑ᫎ/s 20
๒ງ/m 40
3.4

3.2
0.6 0.7 0.8 0.9 1.0 60
sinθ
1460 1480 1500 1520 1540 1560
(b) ܦູງए40 m
ܦᤴ/(mSs -1 )
图 11 阵元数为 32 个时，不同声源深度波束强 (a) ᠇೙एඵ஡
度 - 时间分布图
0
Fig. 11 Beam-time image with different source
depth when the number of array elements is 32
20
将图 11(孔径 217 m) 与图 2(孔径 441 m) 进行
对比可知，当阵列孔径为 217 m 时，波束输出方位 ๒ງ/m 40
谱的主瓣宽度明显增加。两种阵列孔径条件下，水
面声源对应的 H 函数值略有差别，而水下声源对应 60
的 H 函数值则近似不变；由图 12 可知，阵列孔径为
1460 1480 1500 1520 1540 1560
217 m 条件下，H 函数值随声源深度的变化情况与 ܦᤴ/(mSs -1 )
阵列孔径为441 m的H 函数值差异很小。这说明尽 (b) ພᡤࡏඵ஡
管接收阵孔径影响接收阵波束分辨力和空间增益， 图 13 负梯度及温跃层水文环境的声速剖面
但对由波束输出声强提取的能量加权时间特征随 Fig. 13 Sound speed profile of negative gradient
深度的分布关系而言影响较小。 velocity and thermocline