Page 21 - 《应用声学》2021年第1期

第 40 卷 第 1 期 张涛等： 基于光声成像的生物组织微结构定征研究进展 17

光声信号的功率谱性质为解决一系列常规成 关的统计参量，它会随着微结构数量密度的增加
像手段面临的实际难题提供了新的解决方案，这 而单调地增加，因此可定量地衡量微结构的数量
些问题有设备依赖性、微结构尺寸的量化和随机 密度 [63] 。结合了Nakagami形状参数和功率谱斜率
微结构的可重复性实验，以及声学亚波长尺寸结 参数的光声计算机断层成像系统，成功地区分了具
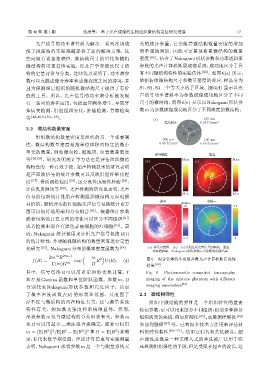
构的定量评估与分类。这些优点说明了，功率谱参 有不同微结构特性的实验仿体 [63] 。如图 6(a) 所示，
数可以克服成像分辨率和成像深度之间的冲突，并 依据仿体微结构尺寸和数量密度的差异，样品分为
且为探测深层组织的随机微结构尺寸提供了有价 S1、S2、S3 三个等大小的子区域。图 6(d) 显示以光
值的工具。所以，光声信号的功率谱分析被发现 声信号功率谱斜率为参数成像成功地区分了不同
有一系列的潜在应用，包括血管网络增生、早期牙 尺寸的微结构，而图 6(e) 显示以 Nakagami 形状参
体病变检测、肝脏组织分化、肿瘤检测、骨骼检查 数m为参数成像成功地区分了不同浓度的微结构。
等 [42,46,51,53−55] 。 (a) 100 µm
ನֶིྟ 0.25˔/mm 3
2.2 微结构数量密度 S2
S1 S3
组织微结构数量密度是组织的另一个重要属
200 µm 100 µm
性。微结构数量密度是指单位体积内特定的微小 0.05˔/mm 3 0.05˔/mm 3
单元的数量，例如微血栓、细胞团、血管数量密度
ηՂࣨϙ ᑟ᧚
等 [26,56] 。研究表明统计学方法也是评估组织微结 (b) Max (c) Max
构特性的一种有效手段。超声检测技术的研究表明
超声回波信号的统计参数可以反映肝脏纤维化程
度 [57] 、骨质疏松程度 [58] 、区分良性或恶性肿瘤 [59] 、
评估乳房肿块等 [60] 。光声检测的研究也表明，光声
Min Min
信号的包络统计性质在检测组织微结构方面也极
பဋ Ԡ஝m
具价值。随机分布的红细胞光声信号包络统计直方 dB/MHz
(d) 0.1 (e) 0.6
图可以很好地用瑞利分布拟合 [41] 。根据统计参数
或者包络统计直方图的变化可以区分不同组织 [61]
或者检测出混合有黑色素瘤细胞的红细胞 [62] 。最
近，Nakagami 统计被用来分析光声信号包络 R(t)
−1.0 0
的统计特性，并对随机微结构的数量密度进行定量
化研究 [63] 。Nakagami分布的概率密度函数为 [64] (a) ನֶᇨਓڏ (b)-(e)Ѭѿ௧̿АܦηՂᄊࣨϙnjᑟ᧚nj
Ҫဋ៨பဋnjNakagamiॎ࿄Ԡ஝m˞Ԡ஝ᄊੇϸፇ౧
m
2m R 2m−1 ( m 2 ) 图 6 混合仿体的多成像参数光声计算机断层成像
f(R) = exp − R U(R), (4)
Γ(m)Ω m Ω 结果 [63]
其中，信号包络 R 可以用希尔伯特变换计算，Γ Fig. 6 Photoacoustic computed tomography
和 U 是 Gamma 函数和单位阶跃函数。参数 m、Ω imaging of the mixture phantom with different
分别代表 Nakagami 形状参数和尺度因子，决定 imaging parameters [63]
了概率密度函数 f(R) 的形状和范围。尺度因子 2.3 微结构弹性
Ω 不仅与微结构的内在特征有关，还与测量系统 组织中微结构的弹性是一个组织特性的重要
特性有关，例如激光强度和系统增益等。然而， 标记参数，它可以用来区分不同组织，识别多种涉及
形状参数 m 仅与微结构的分布形状有关。参数 m 组织病变的疾病，例如肝硬化 [65] 、动脉粥样硬化 [66]
和 Ω 可以用最小二乘法拟合来确定，或者可以用 和前列腺癌 [67] 等。已有很多技术方法用来评估材
m = [E(R )] /E[R − E(R )] 和 Ω = E(R ) 来确 料的弹性特性 [68−71] ，然而它们各有其优缺点。超
2
2
2
2
2
2
定，E 代表数学期望值。理论计算仿真与实验测量 声弹性成像是一种无侵入式的并且被广泛用于临
表明，Nakagami 形状参数 m 是一个与测量系统无 床检测组织弹性的手段，但是受限于超声的波长，这