Page 88 - 《应用声学》2021年第1期

84 2021 年 1 月

入射示意图，图中的圆表示柱形粒子，从图中可以看 为了分析腹壁组织的非均匀性对声场的影响，在
出平面波向前传播，遇到液体柱发生散射、折射等现 图 4(d)∼图4(f)中给出了均匀介质的归一化声压振
象，从而使液体柱受到声辐射力的作用。图 3(b) 展 幅空间分布作为对比。图4(d)为换能器中心频率为
示了时间 t = 40 µs时其声场情况，图3(c)则是转化 1 MHz、3 MHz 时，均匀介质中归一化声压振幅随
成频域中其声场情况。平面入射频率为0.5 MHz，其 声波主传播轴 x 的变化；图 4(e)∼ 图 4(f) 为换能器
余参数设置和文献 [24] 一致。通过 k-Wave 计算所 中心频率为 1 MHz、3 MHz 时，均匀介质中 xy 平面
得无量纲化声辐射力为 0.0039，理论计算为 0.0042， 内归一化声压振幅分布。从图 4 中可以看出，声压
误差为 7.1%，在可接受范围内，验证了 k-Wave计算 振幅在聚焦点的位置达到最大值。对比腹壁组织和
的正确性。 均匀介质中声场情况可以看出，声波在非均匀介质

3.2 腹壁中的声辐射力 中传播，由于介质密度和声速等的变化而产生散射、
为了计算生物组织 (腹壁) 的声辐射力，首先用 反射等现象。对于同一种组织、不同的频率激发下，
k-Wave 对其声场进行仿真，记录整个空间中的声 产生的声场不同。
压以及声速，之后用来计算其声辐射力。仿真模型 在计算声辐射力时，得到了在三维空间网格每
以及计算中所需信息如第 2 节所述。仿真得到该组 个点上的力的 3 个时变分量，然而，在实际的应用
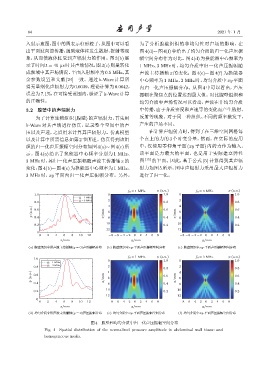
织的归一化声压振幅空间分布如图 4(a)∼图4(c)所 中，仅使用零仰角平面 (xy 平面) 内的力作为输入。
示。图 4(a) 给出了换能器中心频率分别为 1 MHz、 该平面是力最大的平面，也是用于实际建立弹性
3 MHz 时，其归一化声压振幅随声波主传播轴 x 的 图 [15] 的平面。因此，基于公式 (5) 计算得到其声辐
变化；图4(b)∼图4(c)为换能器中心频率为 1 MHz、 射力如图 5 所示，图中声辐射力采用最大声辐射力
3 MHz 时， xy 平面内归一化声压振幅分布。另外， 进行了归一化。

f 0 =1 MHz p (a.u.) f 0 =3 MHz p (a.u.)
1.0 0 1.0 0 1.0
f 0 =1 MHz
0.8 f 0 =3 MHz 2 4 0.8 2 4 0.8
p (a.u.) 0.6 x/mm 6 8 0.6 x/mm 6 8 0.6

0.4
0.4
0.4
10 10
0.2 0.2 0.2
12 12
0
0 2 4 6 8 10 12 -8 -6 -4 -2 0 2 4 6 8 -8 -6 -4 -2 0 2 4 6 8
x/mm y/mm y/mm
(a) ᒌܞጸጻ˗෹ܦฉ˟͜୧ᣉ(y=0)ܦԍ૝ࣨѬ࣋ (b) ᒌܞጸጻ˗xy»ࣱ᭧ܦԍ૝ࣨቇᫎѬ࣋ (c) ᒌܞጸጻ˗xy»ࣱ᭧ܦԍ૝ࣨቇᫎѬ࣋
f 0=1 MHz p (a.u.) f 0=3 MHz p (a.u.)
1.0
0 1.0 0 1.0
f 0 =1 MHz
f 0 =3 MHz
0.8 2 2
0.8 4 0.8
p (a.u.) 0.6 x/mm 6 0.6 x/mm 6 0.6
4
0.4 8 0.4 8 0.4
10 10
0.2 0.2 0.2
12 12
0
0 2 4 6 8 10 12 -8 -6 -4 -2 0 2 4 6 8 -8 -6 -4 -2 0 2 4 6 8
x/mm y/mm y/mm
(d) کӉ̮᠏˗෹ܦฉ˟͜୧ᣉ(y=0)ܦԍ૝ࣨѬ࣋ (e) کӉ̮᠏˗xy»ࣱ᭧ܦԍ૝ࣨቇᫎѬ࣋ (f) کӉ̮᠏˗xy»ࣱ᭧ܦԍ૝ࣨቇᫎѬ࣋
图 4 腹壁和均匀介质中归一化声压振幅空间分布
Fig. 4 Spatial distribution of the normalized pressure amplitude in abdominal wall tissue and
homogeneous media