Page 28 - 《应用声学》2021年第3期

346 2021 年 5 月

得如图 3 蓝色点画线所示的气泡归一化半径随时间 1.4 监测点设置
的演化曲线。为了验证本文仿真模型的可靠性，将 单泡空化过程中泡内和泡外附近流场中各物
本文仿真计算结果与文献 [19]中用实验测试数据拟 理量会发生剧烈变化。在仿真计算过程中，为了监
合的R-P方程的计算结果(图3中的红色点画线)进 测超声激发单泡空化过程中泡内及泡外流体域内
行对比。 压强和密度随时间的变化，在泡内和泡外设置了
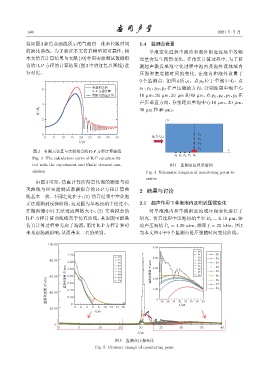
9 个监测点，如图 4 所示。点 p 0 位于单泡中心，点
ࠄᰎલՌᄊ p 1 、p 2 、p 3 、p 4 在声压激励方向，分别距离单泡中心
6
R¹Pவሮᝠካ
దᬍЋ͌ᄾᝠካ 10 µm、20 µm、30 µm 和 40 µm，点 p 5 、p 6 、p 7 、p 8 在
声压垂直方向，分别距离单泡中心 10 µm、20 µm、
4
R⊳R  30 µm和40 µm。

2 y

0 p 
0 5 10 15 20 25 30 35 40 ԍҧК԰
p
t/ms p 

p 
图 3 有限元仿真与实验拟合的 R-P 方程计算曲线 x
p p p p p 

Fig. 3 The calculation curve of R-P equation fit-   
ted with the experiment and Finite element sim- 图 4 监测点位置示意图
ulation Fig. 4 Schematic diagram of monitoring point lo-
cation
由图 3 可知，仿真计算所得空化泡的膨胀与溃
灭曲线与经实验测试数据拟合的 R-P 方程计算曲 2 结果与讨论
线基本一致。不同之处在于：(1) 仿真结果中空化泡
无法观测到反弹阶段，这是因为单泡初始半径过小， 2.1 超声作用下单泡泡内及附近压强变化
在微泡缩小时无法适应网格大小；(2) 实验拟合的 对单泡泡内和单泡附近流域压强变化进行了
R-P 方程计算曲线略高于仿真曲线，其原因可能是 研究。仿真过程中单泡初始半径 R 0 = 6.18 µm，驱
仿真计算过程中考虑了湍流，而用 R-P 方程计算时 动声压幅值 P a = 1.29 atm、频率 f = 25 kHz。图 5
未考虑湍流影响，从而带来二者的差别。 为本文图4中9个监测点处压强随时间变化曲线。

100.00
5.00
p 
1.40 p  p 
4.00 p  p 
p 
80.00 p  p 
1.20 p  3.00 p  p 
p 
p 
p 
p 
p 
p 
p 
0.80
60.00 ᄣ฾གԍू P/atm 1.00 p  ᄣ฾གԍू P/atm 2.00 p  p 
p 
ᄣ฾གԍू P/atm 40.00 0.40 1.00 p 
p 
p 
p 
0.60
p 
0.20
0
t/ms
0 2 4 6 8 10 12 14 16 0 26 28 30 32 34 36 38 40
20.00
t/ms
0
0 5 10 15 20 25 30 35 40
t/ms
图 5 监测点压强变化
Fig. 5 Pressure change of monitoring point