Page 8 - 《应用声学》2021年第3期

326 2021 年 5 月

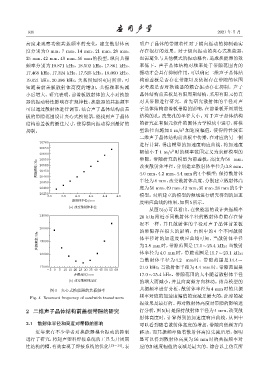
高度来观察功能共振频率的变化，建立散射体高 明声子晶体的带隙特性对于横向振动的抑制确实
度分别为 0 mm、7 mm、14 mm、21 mm、28 mm、 存在很好的效果。对于纵向振动的夹心式换能器，
35 mm、42 mm、49 mm、56 mm 的模型，纵向共振 也需避免与其他模式的振动耦合，造成换能器的效
频率分别为 19.871 kHz、18.502 kHz、17.861 kHz、 率低下。声子晶体结构对频率处于带隙范围内的
17.468 kHz、17.324 kHz、17.525 kHz、18.060 kHz、 振动才会具有抑制作用，可以确定二维声子晶体结
19.021 kHz、20.396 kHz，关系图如图 4(b) 所示，可 构前盖板是否存在带隙以及依据存在带隙的范围
知随着前盖板散射体高度的增加，共振频率先减 来考虑是否对换能器的耦合振动存在抑制。声子
小后增大。研究表明，前盖板散射体的大小对换能 晶体结构前盖板是有限周期结构，采用有限元仿真
器的振动特性影响存在规律性，换能器的共振频率 对其带隙进行研究。首先研究散射体的半径对声
可以通过散射体进行调节，结合声子晶体结构前盖 子晶体结构前盖板带隙的影响，在前盖板开周期性
板的带隙范围设计夹心式换能器，能找到声子晶体 结构的孔，改变孔的半径大小。对于声子晶体结构
结构前盖板的最佳尺寸，使得横向振动得到最好的 的研究在有限元软件的固体力学模块中进行，将模
2
抑制。 型沿径向施加 1 m/s 加速度幅值，使得弹性波在
二维声子晶体结构前盖板中传播，在对应的另一侧
20700
进行计算，得出模型的加速度响应曲线，将加速度
20650
2
幅值小于 1 m/s 时的频率范围定义为求解模型的
20600
20550 带隙。带隙研究的模型为前盖板，高度为 56 mm，
С૝ᮠဋ/Hz 20500 改变散射体半径，分别建立散射体半径为 3.8 mm、
20450
4.0 mm、4.2 mm、4.4 mm 的 4 个模型；保持散射体
20400
半径为 4 mm，改变散射体高度，分别建立散射体高
20350
20300 度为56 mm、49 mm、42 mm、35 mm、28 mm的5个
20250
3.6 3.8 4.0 4.2 4.4 4.6 模型。对所建立的模型的频域进行研究得到的加速
ங࠱ʹӧय़/mm
度响应曲线的结果，如图5所示。
(a) ஈԫங࠱ʹӧय़
从图 5(a) 可以看出，在换能器的设计共振频率
21000
20 kHz 附近不同散射体半径的散射体带隙存在情
况不一样，并且散射体的半径对声子晶体前盖板
20000 的带隙存在很大的影响，由图中的 4 个不同散射
С૝ᮠဋ/Hz 19000 体半径时的加速度响应曲线可知，当散射体半径

为 3.8 mm 时，带隙范围是 17.0 ∼ 25.4 kHz；当散射

18000 体半径为 4.0 mm 时，带隙范围是 15.7 ∼ 23.1 kHz；
当散射体半径为 4.2 mm 时，带隙范围是 14.4 ∼
17000 21.0 kHz；当散射体半径为 4.4 mm 时，带隙范围是
-5 0 5 10 15 20 25 30 35 40 45 50 55 60
नയᰴए/mm 17.0 ∼ 25.4 kHz。带隙范围的大小随着散射体半径
(b) ஈԫங࠱ʹᰴए 的增大而减小，并且向高频方向移动。结合模型的

图 4 夹心式换能器的共振频率 共振频率进行分析，散射体半径为 4 mm 时的共振
频率对应的加速度幅值的衰减是最大的，此时的减
Fig. 4 Resonant frequency of sandwich transducers
振效果是最好的。再对散射体高度对带隙的影响进
2 二维声子晶体结构前盖板带隙的研究 行分析，图5(b)是保持散射体半径为 4 mm、改变散
射体高度时，计算得到的加速度响应曲线，从图中
2.1 散射体半径和高度对带隙的影响 可以看到随着散射体高度的增加，带隙向低频方向
近年来有不少学者对换能器耦合振动的抑制 移动，而共振频率随着散射体高度先减后增，很明
进行了研究，将超声塑料焊接系统的工具头开周期 显可以得到散射体高度为 56 mm 时的共振频率对
性结构的槽，有效实现了焊接系统的优化 [13−14] ，表 应的加速度幅值的衰减是最大的。综合以上仿真所