Page 13 - 《应用声学》2021年第3期

第 40 卷 第 3 期 吴迪等： 在线超声检测系统中螺旋线圈换能器的应用 331

信号为始脉冲，之后为直达横波信号。在电磁超声 时假设电磁铁产生的外磁场在试件表面涡流趋肤
上述参数设定下，压电横波换能器在钢试块各个台 层中垂直均匀分布。由于整个系统具有轴对称特
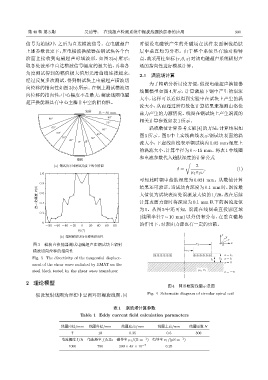
阶面上接收到电磁超声时域波形，如图 3(a) 所示； 点，故采用柱坐标(r, θ, z)对该电磁超声系统辐射声
取各处波形中直达横波信号幅度的极大值，再将各 场的指向性进行模拟计算。
角度测试得到的幅值极大值用光滑曲线连接起来，
2.1 涡流场计算
经过反复多次测试，得到钢试块上电磁超声横波切
为了粗略分析讨论方便，假设电磁超声换能器
向位移的指向性如图3(b)所示。在钢上测试横波切
线圈模型如图 4 所示，计算激励下钢中产生的涡流
向位移的指向性，中心幅度不是最大，螺旋线圈电磁
大小，这样可以近似得到实验中在试块上产生的涡
超声换能器具有中心主瓣非中空的指向性。
流大小，从而通过所得数值计算结果来推测由洛伦
ԧ࠱
R=80 mm 兹力产生的力源情况。线圈在钢试块上产生涡流的
80O
80O 相关计算参数如表1所示。
75O
65O 涡流数值计算参考文献[4]的方法，计算结果如
60O
50O
45O 图 5 所示。图 5 中上实线曲线表示钢试块表面的涡
35O 30O
20O
0O 15O 流大小，下虚线曲线表示钢试块内 0.02 mm 深度上
的涡流大小，计算半径为0 ∼ 15 mm。将表1 中线圈
和电流参数代入趋肤深度的计算公式
ଌஆ
√
(a) ᨂតڱˀՏ฾តᝈएʾᄊԼ᫽᭧ 2
δ = , (1)
1.0 µ 1 σ 1 ω
可知此时钢中趋肤深度为 0.021 mm。从数值计算
0.8 结果还可验证，当试块内深度为 0.1 mm 时，涡流最
ॆʷӑࣨए P↼θ↽ 0.6 大值仅为试块表面处涡流最大值的1/20，故在后续

计算表面力源时将深度为 0.1 mm 以下的涡流近似
0.4
0.2 为 0。从图 5 中还可知，涡流在线圈垂直投影区域
(线圈半径 7 ∼ 10 mm) 以外仍有分布，在垂直磁场
0 的作用下，对表面力源也有一定的贡献。
-80 -60 -40 -20 0 20 40 60 80
θ/(O)
z
(b) ᣣ࠱ഷฉѭՔͯረᄊૉՔভ y
r
图 3 横波直换能器测试电磁超声在钢试块上辐射 r 2 θ x
横波切向位移的指向性 r 1
z/l 2
Fig. 3 The directivity of the tangential displace- l 2 z/l 1
l 1
z/
ment of the shear wave radiated by EMAT on the
steel block tested by the shear wave transducer µ  , σ  z/֓∞

2 理论模型
图 4 圆形螺旋线圈示意图
假设发射线圈为理想中空圆环形螺旋线圈，同 Fig. 4 Schematic diagram of circular spiral coil

表 1 涡流场计算参数
Table 1 Eddy current field calculation parameters

线圈内径/mm 线圈外径/mm 线圈底高/mm 线圈上高/mm 线圈匝数 N
7 10 0.35 0.6 300
电流幅度 I/A 电流频率 f/kHz 磁导率 µ 1 /(H·m −1 ) 电导率 σ 1 /(µS·m −1 )
1000 750 200 × 4π × 10 −7 6.25