Page 18 - 《应用声学》2021年第3期

336 2021 年 5 月

0 引言 高 的 时 域 有 限 差 分 法 (Finite-difference time-

domain, FDTD) [11] 来完成的。所用到的波场计算
井间地震，顾名思义，就是在两口井中分别放
公式是弹性波的一阶速度-应力方程，区域边界产生
置震源 (激发信号) 和检波器 (接收信号)，通过对检
的强反射采用完全匹配层 (Perfect matched layer,
波器获得的信号进行分析处理，来得到两井之间地
PML) [12] 进行吸收。以图1的多层地质模型为例，进
质结构的一种地震勘探方法。井间地震的资料处理
行井间地震的数值模拟。
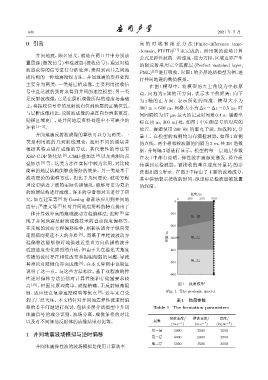
主要分为两类：一类是层析成像，主要利用接收信 在图 1 模型中，将模型的左上角设为坐标原
号中直达波的到时来得到井间的速度模型；另一类
点，向右为 x 轴的正方向，表示水平的距离；向下
是反射波成像，它是在层析成像所得的速度场基础
为 z 轴的正方向，表示所处的深度。模型大小为
上，将接收信号中的反射波归位到地层的正确位置。 300 m × 600 m，网格大小为 ∆x = ∆z = 0.5 m，时
与层析成像相比，反射波成像的垂直向分辨率更高、 间间隔约为57 µs，最大的记录时间是0.4 s。震源坐
勘探区域更广，是井间地震资料处理中不可缺少的 标在 (0 m, 300 m) 处，如图 1 中左侧星号所对应的
环节 [1−2] 。 位置。震源使用 200 Hz 的雷克子波，加载到 V x 分
井间地震反射波成像的算法可以分为两类。一 量上。在模型的右侧均匀布满检波器，如图 1 右侧
类是利用波的几何射线理论，选用不同的道集并 的点线。两个相邻检波器的间隔为2 m，共301道数
根据其特点进行成像的方法。其代表性的算法有 据，并每隔 3 道进行显示。模型的每一层地层参数
XSP-CDP转化法 [3] 、CMD叠加法 [4] 以及共测向点 在表 1 中都有说明。弹性波在震源处激发，经介质
叠加法 [5] 等。这类方法在实际中较为常用，对比较 传播到达检波器。被接收的垂直速度分量 V z 的示
简单的地层结构能够获得好的效果。另一类是基于 意图如图 2 所示。在图 2 中标出了主要的波场成分，
波动理论的偏移方法。相比于几何理论，波动方程 其中横轴表示接收的时间，纵坐标是检波器被放置
理论更贴近于波的实际传播情况，能够对更为复杂 的深度。
的地层结构进行成像。许多的学者都对其进行了研
ᡰሏ/m
究，如左建军等 [6] 将 Gazdag 相移法应用到井间地 0 100 200 300
0
震中；严建文等 [7] 针对井间地震资料的特点提出了
一种计算效率高的炮域波动方程偏移法；张辉 [8] 实 100
ኄʷࡏ
现了井间地震反射波成像技术的叠前深度偏移等。
200
在常规的波动方程偏移法中，相移法适合于纵向变
速而横向变速不大的介质 [6] 。而基于单程波波动方 ງए/m 300 ኄ̄ࡏ
程偏移法能够很好地描述近垂直方向传播的波并
适应速度变化剧烈的介质，但由于其在描述大角度 400
传播的波时存在相位改变和振幅削弱的问题，导致
ኄʼࡏ
其难以对陡倾角界面成像 [9] ，在本文算例中也验证 500
说明了这一点。与这些方法相比，基于双程波的弹
600
性逆时偏移方法虽然对计算性能和存储量要求较
高 [10] ，但因其原理简单、成像精确、无反射倾角限 图 1 地质模型
制、适应任意复杂速度模型等优点 [9] ，近年来已受 Fig. 1 The geologic model
到了广泛关注。本文将针对井间地震弹性波逆时偏 表 1 地层参数
移的若干问题进行探讨，包括多层介质模型中井间 Table 1 The formation parameters
地震信号的成分识别、波场分离、成像条件的对比
纵波速度/ 横波速度/ 密度/
以及对不同倾角反射体的成像结果对比等。 层数
(m·s −1 ) (m·s −1 ) (kg·m −3 )
第一层 3000 2000 2000
1 井间地震波场模拟与逆时偏移
第二层 4000 2800 2500
第三层 5000 3500 3000
井间地震弹性波的波场模拟是使用计算效率