Page 150 - 《应用声学》2022年第1期

146 2022 年 1 月

保理想的声束聚焦性能，因此不再对阵元数进行深 的纵向分辨能力。
入的讨论分析。本文主要从以下两个方面分析声束 数值模拟中的参数选择如下，固体介质选择为
聚焦性能：焦距处的周向声场分布、沿偏转角的声 钢，其纵横波声速分别为5778 m/s 和 3194 m/s，中
场分布，前者用于分析聚焦声场指向性、栅瓣、旁瓣 心频率为 5 MHz。为了更真实地模拟瞬态声场，采
等问题，表征了聚焦声束的周向分辨能力；后者用于 用余弦包络函数作为阵元激励信号：
分析焦点周围的声能量波动情况，表征了聚焦声束

 { [ ( )]} [ ( )]
 1 2π t c t c
 1 + cos t − cos 2πf 0 t − , 0 6 t 6 t c ,
f(t) = 2 t c 2 2 (9)

0, t < 0, t > t c .

其中：f 0 是信号的中心频率，t c 是信号的时间宽度。 的栅瓣，其原因是瞬态波限制了声波干涉的产生条
件，从而阻止了栅瓣的形成。
2.1 阵元间距

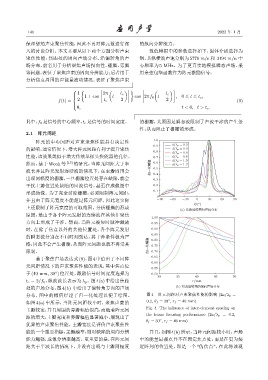
阵元的中心间距对声束聚焦性能具有决定性 1.0
0.9 d⊳λ p=0.2
的影响，通常情况下，增大阵元间距有利于提升聚焦 d⊳λ p =0.4
0.8 d⊳λ p=0.6
性能，该效果类似于增大传统单探头换能器的孔径。 0.7 d⊳λ p =0.8
然而，基于 Wooh 等 [15] 的研究，当阵元间距大于半 0.6 d⊳λ p =1.0
d⊳λ p=1.2
波长并且阵元发射连续波的情况下，在主瓣周围会 ॆʷӑࣨϙ 0.5
0.4
出现同幅度的栅瓣，一旦栅瓣位置处存在缺陷，就会 0.3
干扰主瓣位置处缺陷的回波信号，甚至在成像图中 0.2
形成伪像。为了完全消除栅瓣，必须限制阵元间距， 0.1
0
并且由于阵元宽度不能超过阵元间距，因此这实际 -90 -60 -30 0 30 60 90
θ/(°)
上还限制了阵元宽度的可取范围。分析栅瓣的形成
(a) ཥᡰܫᄊևՔܦڤѬ࣋
原因，是由于各个阵元发射的连续波在其他非聚焦
1.00
方向上形成了干涉。然而，当阵元被短时脉冲激励 0.95
时，在除了焦点以外的其他位置处，各个阵元发射 0.90
0.85
的瞬态波分别在不同时刻到达，其干涉条件极为严 0.80
格，因此不会产生栅瓣，从而阵元间距也就不再受其 ॆʷӑࣨϙ 0.75
限制。 0.70
基于聚焦声场表达式(8)，图4 中给出了不同阵 0.65
0.60
元间距情况下的声束聚焦性能的表现，其中焦点位
0.55
于(40 mm, 30 ) 位置处，激励信号时间宽度选择为 0.50
◦
30 35 40 45 50
t c = 2/f 0 ，纵波波长表示为 λ p 。图 4(a) 中给出焦距 r/mm
处的声场分布，图4(b) 中给出了偏转角方向的声场 (b) ෹ᅌϠᣁᝈᄊጫՔܦڤѬ࣋
分布，图中的幅值经过了归一化处理以便于绘图。 图 4 阵元间距对声束聚焦性能的影响 (2a/λ p =
◦
如图 4(a) 中所示，当阵元间距较小时，聚焦声束的 0.2, θ f = 30 , r f = 40 mm)
主瓣较宽，并且周围的旁瓣幅值很高，而随着阵元间 Fig. 4 The influence of inter-element spacing on
the beam focusing performance (2a/λ p = 0.2,
距的增大，主瓣宽度和旁瓣幅值显著减小，展现出了
θ f = 30 , r f = 40 mm)
◦
优异的声束聚焦性能。主瓣宽度是评价声束聚焦性
能的一个重要指标，主瓣越窄，则对缺陷的周向分辨 并且，如图 4(b)所示，当阵元间距较小时，声场
能力越强，成像分辨率越高。更重要的是，在阵元间 中的能量最强点并不在预定焦点处，而是在更为接
距大于半波长的情况下，并没有出现与主瓣同幅度 近阵列的位置处，即是一个 “伪焦点”，在此将该现