Page 136 - 《应用声学》2022年第3期

458 2022 年 5 月

2.3 超声波波形能量变化规律 频率段信号能量呈指数递减；在500 ∼ 1000 kHz 能
波形的能量用 P 来量化，以无量纲的形式呈现， 量变化不大。可见不同种类砂岩超声波信号随入射
定义为平方整流振幅下面积的积分 [16] ： 频率能量的衰减表现具有差异性，信号能量在相对
∫ 低的频率范围影响较大，在高频的超声波频率下，信
2
P = A dt, (3)
V
号能量趋于稳定。
式 (3) 中：P 为波形能量；A V 为波形幅值；t 为信号
由图 10 可知：入射频率越高，能量衰减越大；
采集时长。通过式(3)计算出波形能量，比较入射频
50 kHz 入射频率下穿透岩样后的能量明显高于其
率、孔隙率与波形能量均值的关系，分别见图 9 和
他入射频率下的信号能量；50 kHz 与 100 kHz 频率
图 10。
的测试结果与更高频率的测试结果相比更加离散，
18000 200 kHz 以及更高频率的测试结果更为聚集，各频
16000 ༦ᆋࡸฉᑟکϙ 率段信号能量差距较小，入射频率对信号能量的影
ጚᆋࡸฉᑟکϙ
14000
ᜢᆋࡸฉᑟکϙ 响力减弱，能量随孔隙率的衰减度趋于稳定。
12000
ᑟ᧚/V 2 10000 2.4 超声波主频幅值变化规律
8000
6000 为进一步分析砂岩岩样对声波的滤波作用，将
接收到的超声波信号进行FFT为频域信号，考察其
4000
入射频率对超声波信号主频幅值的影响。为方便展
2000
示，选取其中5 个岩样，其主频幅值随入射频率变化
0
见图11。随入射频率升高，主频幅值均递减，这与上
0 200 400 600 800 1000
ᮠဋ/kHz 文超声波波能与入射频率的实验结果相似：50 kHz
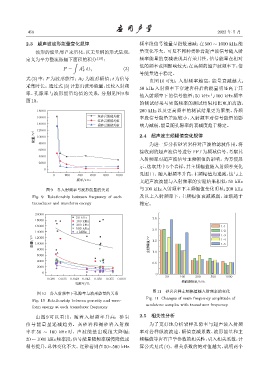
图 9 各入射频率与波形能量的关系 与100 kHz入射频率下主频幅值变化明显；200 kHz
Fig. 9 Relationship between frequency of each 及以上入射频率下，主频幅值衰减减弱，逐渐趋于
transducer and waveform energy 稳定。

20000
50 kHz 2.5
18000 100 kHz
16000 200 kHz 1-1
500 kHz 2.0
14000 1 MHz 1-2
1-3
ᑟ᧚/V 2 10000 ˟ᮠࣨϙ/V 1.5 1-4
12000
1-5
8000 1.0
6000
4000
0.5
2000
0
0
50 100 200 500 1000
0.030 0.035 0.040 0.045 0.050 0.055 0.060
૱ᑟ٨ᮠဋ/kHz
ߘᬩဋ/%
图 11 砂岩岩样主频幅值随入射频率的变化
图 10 各入射频率下孔隙率与波形能量的关系
Fig. 11 Changes of main frequency amplitude of
Fig. 10 Relationship between porosity and wave-
sandstone samples with transducer frequency
form energy at each transducer frequency
由图 9 可以看出，随着入射频率升高，砂岩 2.5 相关性分析
信号能量呈递减趋势。灰砂岩和褐砂岩入射频 为了更好地分析岩样孔隙率与超声波入射频
率在 50 ∼ 100 kHz 时，声波能量出现很大降幅； 率对岩样纵波波速、幅值衰减系数、波形能量和主
20 ∼ 1000 kHz频率段，信号能量随频率缓慢降低或 频幅值等岩石声学参数的相关性，引入相关系数，计
稍有提升，总体变化不大。红砂岩则在 50∼500 kHz 算公式见式 (4)。相关系数的绝对值越大，说明两个