Page 36 - 《应用声学》2022年第5期

712 2022 年 9 月

其中，f 是入射声波频率。在均匀介质中，由于均匀 ∆s k ∑ w ij ∆T i / N
N
∑
j
介质内部声速分布恒定，具有相同扰动时间的散射 s k+1 = T obs w ij , (3)
i i=1 i i=1
点呈对称分布，所以均匀介质中发射点与接收点之
其中，i、j 和 k 分别表示收发探头对、网格点和迭代
间的菲涅尔区域呈椭圆形状。当介质中出现不均匀
k
k
的后缀，s k+1 = s + ∆s ，∆T 是由如式 (4) 表示的
j
i
j
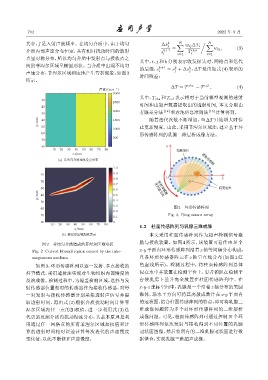
声速分布，菲涅尔区域相应地产生弯折现象，如图 2
时间残差：
所示。
∆T = T obs − T cal , (4)
ܦᤴ/(mSs -1 )
3000
其中，T obs 和 T cal 表示相对于当前模型观测的透射
10
2500
20 时间和由超声数据提取出的透射时间, 本文分别由
2000 有限差分法 [14] 和赤池信息准则法 [15] 计算得到。
30
y/mm 40 1500 随着迭代次数不断增加，当 ∆T 开始增大时停
50
1000 止更新慢度。由此，采用菲涅尔区域法，建立基于环
60 形传感阵列的乳腺二维层析成像方法。
500
70
80 y
10 20 30 40 50 60 70 80 ˾ᒍጸጻ
x/mm
(a) ᭤کӉ̮᠏ԣஆԧགѬ࣋ ଌஆ͜ਖ٨
1.0
0.9
10
O
0.8 x
20
0.7
30 0.6 ԣੳಊவՔ Ⴡԫጸጻ
y/mm 40 0.5
ԧ࠱͜ਖ٨
50 0.4
0.3
60 图 3 环形传感阵列
0.2
70 Fig. 3 Ring sensor array
0.1
80 0
10 20 30 40 50 60 70 80 1.2 柱面传感阵列与乳腺三维成像
x/mm
(b) ᖧ๖࠷ӝ۫ҫి᛫ᇨ 本文采用柱面传感阵列作为超声检测信号激
励与接收装置。如图 4 所示，该装置可看作由 N 个
图 2 非均匀介质造成的菲涅尔区域弯折
Fig. 2 Curved Fresnel region caused by the inho- x-y 平面内环形传感阵列沿着 z 轴等间隔分布构成，
mogeneous medium 且各环形传感器阵元在 z 轴呈直线分布 (如图 3 红
如图 3，环形传感阵列以逐一发射、多点接收的 色虚线所示)。检测过程中，将柱面传感阵列总体
扫查模式，采用透射法实现对生物组织内部慢度的 浸在水中并放置在检测平台上，患者俯趴在检测平
反演成像。检测过程中，为覆盖检测区域，选择与发 台使乳房下垂并完全放置在柱面传感阵列中。在
射传感器位置相对的传感器作为接收传感器，对每 x-y-z 坐标空间中，乳腺是一个沿着 z 轴分布的类圆
一对发射与接收传感器分别采集透射声信号并提 锥体，沿水平方向可将其离散成数片在 x-y 平面内
取透射时间，再由式 (2) 根据介质扰动时间计算菲 的冠状面，结合柱面传感阵列的特点，即可将乳腺三
涅尔区域内任一点的加权值，进一步利用式 (3) 迭 维成像问题转为多个对环形传感阵列的二维层析
代更新反演介质内扰动慢度分布，其基本原理是利 成像问题。可见，柱面传感阵列可通过控制 N 个环
用通过任一网格点的所有菲涅尔区域加权值和计 形传感阵列依次发射与接收得到不同位置的乳腺
算的透射时间相对误差计算每次迭代的声速慢度 冠状面图像，然后将所有的二维乳腺冠状面进行数
变化值，以此不断修正声速慢度。 据整合，实现乳腺三维超声成像。