Page 31 - 《应用声学》2022年第5期

第 41 卷 第 5 期 闫博等： 流动微泡群瞬态空化强度时域分布的比例反馈调节 707

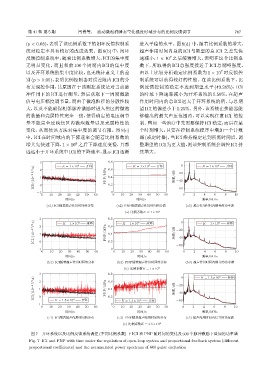
(p < 0.05)，表明了该比例系数下的闭环反馈控制系 进入平稳的水平。图8(d) 中，随着比例系数的增大，
统对稳定率具有较好的改进效果。图 8(b) 中，闭环 超声作用时间内总的 ICI 与期望的总 ICI 之差先快
7
反馈控制系统中，随着比例系数增大，ICI 的集中度 速减小，1 × 10 之后缓慢增大，表明在这个比例系
无明显变化，而且和前 100 个周期内 ICI 的集中度 数下，所取得的 ICI 总强度接近于 ICI 总期望强度。
7
以及开环系统的集中度比较，也无统计意义上的差 由以上比较分析确定比例系数为 1 × 10 时反馈控
别(p > 0.05)，表明比例控制器对误差限内 ICI的分 制系统可以获得较好的性能。在该比例系数下，比
布无调控作用，其原因在于该测控系统是对当前脉 例反馈控制的稳定率达到期望水平 (49.28%)，ICI
冲作用下的 ICI 进行测量，然后获取下一周期激励 的时域下降速率减小为开环系统的 5.59%，在超声
信号电压幅度调节量，而由于微泡粒径的分散性较 作用时间内的总 ICI 远大于开环系统的值，与总期
大，以及不能确保相邻脉冲激励时进入焦区的微泡 望ICI的偏差小于 1.25%。另外，该系统在换能器能
的数量和壳层特性完全一致，使得确定的电压调节 够输出的最大声压范围内，可以实现任意 ICI 的控
量不能完全反映焦区内微泡数量以及壳层特性的 制。譬如一些治疗中先需要保持ICI稳定，而后在某
变化，从而使该方法对集中度的调节有限。图 8(c) 个时刻增大，只要在控制系统程序中增加一个计数
中，ICI 在时间域内的下降速率会随着比例系数的 器(或定时器)，当 ICI 维持稳定达到所需时间后，调
6
增大先快速下降，1 × 10 之后下降速度变慢，且都 整期望的ICI为更大值，则该控制系统会调控ICI持
远远小于开环系统中ICI的下降速率，显示ICI逐渐 续增大。

3 K=1f10 5 नဗ 0.8 K=1f10 5 नဗ 0 K=1f10 5 नဗ
ICI/(10 -9 V 2 Ss) 2 1 0 PNP/MPa 0.4 Ҫဋ/dB -20
0.6

-40
0.2
-1 0 -60
0 10 20 30 40 50 60 0 10 20 30 40 50 60 0 2 4 6 8 10
௑ᫎ/s ௑ᫎ/s ᮠဋ/MHz
(a1) ICIᬤᅌᡔܦͻၹ௑ᫎᄊѬ࣋ (a2) PNPᬤᅌᡔܦͻၹ௑ᫎᄊѬ࣋ (a3) ᡔܦͻၹ௑ᫎЯηՂᄊҪဋ៨
(a) උΓጇ஝K=1f10 5
3 K=1f10 7 नဗ 0.8 K=1f10 7 नဗ 0 K=1f10 7 नဗ
ICI/(10 -9 V 2 Ss) 2 1 PNP/MPa 0.6 Ҫဋ/dB -20

0.4
-40
0.2
0
-60
-1 0
0 10 20 30 40 50 60 0 10 20 30 40 50 60 0 2 4 6 8 10
௑ᫎ/s ௑ᫎ/s ᮠဋ/MHz
(b1) ICIᬤᅌᡔܦͻၹ௑ᫎᄊѬ࣋ (b2) PNPᬤᅌᡔܦͻၹ௑ᫎᄊѬ࣋ (b3) ᡔܦͻၹ௑ᫎЯηՂᄊҪဋ៨
(b) උΓጇ஝K=1f10 7
3 0.8 0 K=1.5f10 8 नဗ
ICI/(10 -9 V 2 Ss) 2 1 PNP/MPa 0.6 Ҫဋ/dB -20

0.4
-40

-1 0 K=1.5f10 8 नဗ 0.2 0 K=1.5f10 8 नဗ -60
0 10 20 30 40 50 60 0 10 20 30 40 50 60 0 2 4 6 8 10
௑ᫎ/s ௑ᫎ/s ᮠဋ/MHz
(c1) ICIᬤᅌᡔܦͻၹ௑ᫎᄊѬ࣋ (c2) PNPᬤᅌᡔܦͻၹ௑ᫎᄊѬ࣋ (c3) ᡔܦͻၹ௑ᫎЯηՂᄊҪဋ៨
(c) උΓጇ஝K=1.5f10 8

图 7 开环系统以及比例反馈系统调控 (不同比例系数) 下 ICI 和 PNP 随时间的变化及 600 个脉冲激励下叠加的功率谱
Fig. 7 ICI and PNP with time under the regulation of open-loop system and proportional feedback system (different
proportional coefficients) and the accumulated power spectrum of 600 pulse excitation