Page 154 - 《应用声学》2022年第6期

1000 2022 年 11 月

[ ]
1 tan(kt/2)
Z = 1 − k 2 33 , (5) 500 1-3یԍႃܭՌెந
jωC 0 kt/2 1-3یԍႃܭՌెநԍႃ࠵ಏ
450
D
2
S
式 (5) 中：k 2 = h /β c ，k 33 为厚度振动的机电
33 33
33
33
耦合系数；ω 为角频率。当压电小柱谐振时，Z = 0， 400
tan(kt/2) ៈ૝ᮠဋ/kHz
则可得到 → 1。 350
kt/2
1.2 1-3型压电复合材料分析 300
250
1-3 型压电复合材料由一维分布的压电陶瓷柱
以及三维分布的聚合物组成，因而其相关等效参数 200 4 5 6
的表达式主要由压电陶瓷相的体积分数、压电陶瓷 Ԓए/mm
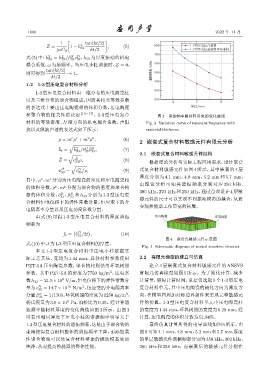
和聚合物的相关性质决定 [15−17] 。1-3 型压电复合 图 3 谐振频率随材料厚度的变化曲线
材料的等效密度、厚度方向的机电耦合系数、声阻 Fig. 3 Variation curve of resonant frequency with
抗以及纵波声速的表达式如下所示： material thickness

p p
c c
¯ ρ = m ρ + m ρ , (6)
2 嵌套式复合材料敏感元件有限元分析
√
¯
h /¯c β ,
k t = ¯2 D ¯S (7)
33 33 33
2.1 嵌套式复合材料敏感元件结构
√
¯
D
Z = ¯ c ¯ρ, (8) 根据理论分析与实际工程应用需求，设计嵌套
33
√ /
D
¯ v 33 = ¯ c D ¯ ρ, (9) 式复合材料敏感元件如图 4 所示，其中嵌套的 4 层
33
厚度分别为 4.1 mm、4.8 mm、5.2 mm 和 5.7 mm，
其中，ρ 、m 分别为压电陶瓷的密度和压电陶瓷相
c
c
由理论分析可知其谐振频率分别对应 350 kHz、
p
的体积分数，ρ 、m 分别为聚合物的密度和聚合物
p
300 kHz、270 kHz 和250 kHz，通过合理设计 4 层敏
¯
¯S
相的体积分数，¯c 、β 和 h 33 分别为 1-3 型压电复
D
33
33
合材料恒电位移下的弹性常数分量、恒应变下的介 感元件的尺寸可以实现不同振动模态的耦合，从而
实现换能器工作带宽的拓展。
电隔离率分量以及压电劲度常数分量。
由式 (9) 可得 1-3 型压电复合材料的厚度谐振 ԍႃᬝၬ ဗතಞᑠ
频率为
( D )
f t = ¯v /2t , (10)
33
图 4 嵌套式敏感元件示意图
式(10)中，t为1-3型压电复合材料的厚度。
Fig. 4 Schematic diagram of nested sensitive element
本文 1-3 型压电复合材料中压电小柱依据实
际工艺其长、宽均为 1.44 mm，具体材料参数使用 2.2 有限元模型的建立与仿真
PZT-5A 压电陶瓷参数，聚合物相则使用环氧树脂 建立 4 层嵌套式复合材料敏感元件的 ANSYS
参数。其中 PZT-5A 的密度为 7750 kg/m ，压电常 有限元仿真模型如图 5 所示。为了简化计算，减少
3
数h 33 = 21.5×10 V/m，恒电位移下的弹性常数分 计算量，缩短计算时间，单层仅选取 5 个 1-3 型压电
8
2
量为c D = 14.7 × 10 10 N/m ，恒应变的介电隔离率 复合材料单元，其中压电陶瓷的极化方向为厚度方
33
3
分量β S = 1/1700，环氧树脂的密度为1250 kg/m ， 向，在模型四周加对称边界条件来实现完整敏感元
33
9
杨氏模量为 3.6 × 10 Pa，泊松比为 0.35。经计算谐 件的仿真。1-3 型压电复合材料单元中压电陶瓷柱
振频率随材料厚度的变化曲线如图 3 所示。由图 3 的宽度为 1.44 mm，环氧树脂的宽度为0.28 mm，经
可看出相同厚度下压电小柱的谐振频率明显大于 计算，压电陶瓷的体积分数为51.84%。
1-3型压电复合材料的谐振频率，这是由于聚合物的 最终仿真计算所得的电导曲线如图 6 所示，由
束缚使得复合材料整体的谐振频率下降，而添加柔 图 6 可知 4.1 mm、4.8 mm、5.2 mm 和 5.7 mm 厚度
性聚合物也可以使复合材料整体的振动模态更加 的单层敏感元件谐振频率分别为350 kHz、302 kHz、
纯净，从而提高换能器的整体性能。 280 kHz 和 254 kHz，而嵌套后的敏感元件分别在