Page 168 - 《应用声学》2022年第6期

1014 2022 年 11 月

จ೟1 จ೟2 จ೟3 基于不同尺寸的抗风噪结构，进行声波传递损
失实验。以截止频率评价其效果，显然截止频率越
低，传递损失越大。传声器和不同参数的结构耦合，
如图7固定在支架上，两种结构参数如表1所示。内
部均填充密度为 18 kg/m 的相同泡棉。同时根据
3
公式 (4) 和公式 (5) 计算出两种结构下的理论截止
频率，见表 1。在消声室中音箱发出 50 ∼ 10000 Hz
ࠛए὘จ೟1 จ೟2 จ೟3 的扫频信号，Audio Precision 5.0 声频测量设备录
图 11 3 种不同密度的泡棉 取并分析传声器拾取到的信号。
Fig. 11 Three different kinds of foams
表 1 实验结构参数
-20 Table 1 The parameters of two different
-30 structures
-40 腔体 管道等效 管道 理论截止
ࣨϙ/dB -50 体积/mm 3 直径/mm 长度/mm 频率/Hz
-60
-70 จ೟1 结构 1 353 0.6 8.5 1060
จ೟2
-80 จ೟3 结构 2 31 0.6 4.5 4932
-90
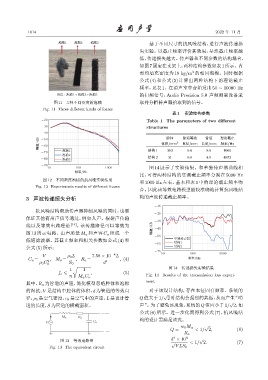
10 100 1000 图 14 展示了实验结果。和单独传声器曲线相
ᮠဋ/Hz
比，可得两种结构的实测截止频率分别在 5000 Hz
图 12 不同密度泡棉的抗风噪实验结果
和 1000 Hz 左右，基本和表 1 中的理论截止频率吻
Fig. 12 Experiments results of different foams
合。因此该等效电路模型能较准确地计算抗风噪结
3 声波传递损失分析 构的声波传递截止频率。

-15
抗风噪结构帮助传声器抑制风噪的同时，也要
-25
保证其他有用声信号通过，例如人声。根据声传输
-35
线以及等效电路理论 [14] ，该传播路径可以等效为 ࣨϙ/dB -45
图 13 所示电路。由声质量 M a 和声容 C a 组成一个
-55
低通滤波器。其截止频率和相关参数如公式 (4) 和 ӭ࿘͜ܦ٨
-65 ፇ౞1
公式(5)所示： ፇ౞2
-75 50 500 5000
V ρ 0 L 7.58 × 10 −4 L
C a = 2 , M a = , R a = , (4) ᮠဋ/Hz
ρ 0 C S 0 d 4
0
√ 图 14 传递损失实验结果
1 1
f c 6 , (5)
π M a C a Fig. 14 Results of the transmission loss experi-
其中，R a 为管道的声阻，简化模型忽略腔体和泡棉 ment
的阻抗；V 是结构中腔体的体积，d 为管道的等效直 对于该设计结构，存在本征固有频率。系统的
√
径，ρ 0 是空气密度，c 0 是空气中的声速，L 是设计管 Q 值大于1/ 2 时结构会强烈的共振，从而产生“哨
√
道的长度，S 为管道的横截面积。 声”。为了避免该现象，系统的Q值应小于 1/ 2，如
公式 (6) 所示。进一步化简得到公式 (7)，抗风噪结
M a R a
构的设计需满足该式。
p ~ C a
√
w 0 M a
Q = < 1/ 2, (6)
R a
4
图 13 等效电路图 d × 10 6 √
√ < 1/ 2. (7)
Fig. 13 The equivalent circuit V LS 0