Page 140 - 《应用声学》2023年第1期

136 2023 年 1 月

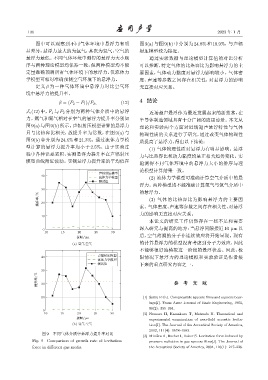
图中可以观察到不同气体环境中悬浮力有明 图 9(a) 与图 9(b) 中分别为 24.8% 和 18.9%，与声辐
显差异，悬浮力最大的为氩气，其次为氦气，空气的 射压模型较为接近。
悬浮力最低。不同气体环境中测得的悬浮力大小顺 通过实验数据与理论模型计算值的对比分析
序与两种理论模型均保持一致，但两种模型均不能 可以推断，特定气体的比热容比为影响悬浮力的主
定量准确预测所有气体环境下的悬浮力，仅流体力 要因素，气体动力黏度对悬浮力影响较小。气体密
学模型可相对准确预测空气环境下的悬浮力。 度、声速等参数之间存在相关性，对悬浮力的影响
定义 β 为一种气体环境中悬浮力对比空气环 无直接对应关系。
境中悬浮力的提升率，

β = (F 2 − F 1 )/F 2 , (12) 4 结论
式 (12) 中，F 1 与 F 2 分别为两种气体介质中的悬浮 近场超声悬浮作为最近发展起来的新技术，在
力。氩气和氦气相对于空气的悬浮力提升率分别如 半导体制造领域具有十分广阔的应用前景。本文从
图9(a)与图9(b)所示。声辐射压模型计算的悬浮力 理论和实验两个方面对近场超声悬浮特性与气体
只与比热容比相关，故提升率为常数，在图 9(a) 与 物理性质的关系进行了研究，通过改变气体物理性
图 9(b) 中分别为 24.6% 和 21.3%。通过流体力学模 质提高了悬浮力，得出以下结论：
型计算的悬浮力提升率均小于 2.5%。由于实验过 (1) 气体物理性质对悬浮力有明显影响。悬浮
程中各种误差累积，实测悬浮力提升率在声辐射压 力与比热容比和动力黏度均呈正相关趋势变化。实
模型曲线附近波动。实测悬浮力提升率的平均值在 验测得不同气体环境中的悬浮力大小的排序与理
论模型计算结果一致。
ܦᣣ࠱ԍവی
40 ืʹҧߦവی (2) 流体力学模型可准确计算空气介质中的悬
฾តϙ
浮力。两种模型均不能准确计算氩气与氦气介质中
30 的悬浮力。
ଢӤဋ/% 20 素。气体密度、声速等参数之间存在相关性，对悬浮
(3) 气体的比热容比为影响悬浮力的主要因

力的影响无直接对应关系。
10
本论文的研究工作仍然存在一些不足和需要
深入研究与提高的地方：当悬浮间隙接近 10 µm 以
0
10 15 20 25 30
后，空气薄膜的分子非连续效应将开始显现。现有
૝ࣨ/µm
(a) දඡ-ቇඡ 的计算悬浮力的模型没有考虑到分子力效应，因此
不能够很好地模拟这一阶段的悬浮状态。因此，极
ܦᣣ࠱ԍവی
40 限情况下悬浮力的理论模拟和实验验证是作者接
ืʹҧߦവی
฾តϙ 下来的重点研究内容之一。
30
ଢӤဋ/% 20 参 考 文 献

10 [1] Salbu E O J. Compressible squeeze films and squeeze bear-
ings[J]. Trans Asme Journal of Basic Engineering, 1963,
86(2): 355–364.
0
10 15 20 25 30 [2] Nomura H, Kamakura T, Matsuda K. Theoretical and
૝ࣨ/µm experimental examination of near-field acoustic levita-
(b) ඬඡ-ቇඡ tion[J]. The Journal of the Acoustical Society of America,
2002, 111(4): 1578–1583.
图 9 不同气体介质中悬浮力提升率对比
[3] Minikes A, Bucher I, Haber S. Levitation force induced by
Fig. 9 Comparison of growth rate of levitation pressure radiation in gas squeeze films[J]. The Journal of
force in different gas media the Acoustical Society of America, 2004, 116(1): 217–226.