Page 90 - 《应用声学》2023年第1期

86 2023 年 1 月

式(2) 中，NI 代表线圈提供的激励安匝数，H i 、l i 分 表 1 导磁件不同磁导率对应的铁镓磁场强度
别是第 i 段均匀磁路中的磁场强度和长度，Φ B 代表 Table 1 The magnetic field strength of
磁路中的磁通量。由式 (2) 可以得出铁镓棒上的磁 iron gallium corresponding to different
场强度H 1 为 magnetic permeability of magnetic con-
ductive parts
Φ B R 1
H 1 = =
l 1
导磁件磁导率 铁镓材料内部磁场强度/(A·m −1 )
NI (R 1 + R 1w ) (R 2 + R 2w ) R 1
. (3)
[R 1 R 1w (R 2 + R 2w ) + R 2 R 2w (R 1 + R 1w )] l 1 1.2 6666
线圈匝数取 640，电流取 12 A，空气的相对磁 5 17163
导率为 1，铁镓的相对磁导率取 100，铁镓棒的总长 20 28686
度取 200 mm，导磁件的总长度取30 mm，两种元件 100 34039
半径相同取 15 mm，空气域厚度取 10 mm。计算铁 10000 39085
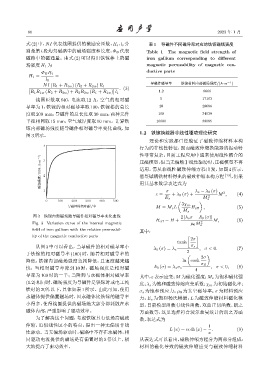
镓内部磁场强度随导磁件相对磁导率变化曲线，如
1.2 铁镓换能器非线性驱动理论研究
图 3所示。
理论和实践都已经验证了磁致伸缩材料本构
4
行为的非线性特征，因而磁致伸缩换能器的振动特
性非常复杂，目前工程应用中通常使用线性耦合的
ᇓڤूए/(104 ASm -1 ) 2 适用，需从非线性磁致伸缩方程出发，如图 4 所示，
3
压磁模型，但当无偏场非线性驱动时，压磁模型不再

[13]
，仍采
借鉴铽镝铁材料得出的磁致伸缩本构方程
σ
1 用其基本数学表达式为 λ s − λ 0 (σ)
2
ε = + λ 0 (σ) + 2 M , (4)
E s M s
0 100 200 300 400 500 ( )
࠮ᇓ͈ᄊᄱࠫᇓ࠮ဋ M = M s L 3χ m H eff , (5)
M s
图 3 铁镓内部磁场随导磁件相对磁导率变化曲线 2 [λ s σ − Λ 0 (σ)]
H eff = H + M, (6)
Fig. 3 Variation curve of the internal magnetic µ 0 M s 2
field of iron gallium with the relative permeabil-
其中：
ity of the magnetic conductive parts [ ]
2σ
tanh
从图 3 中可以看出，当导磁件的相对磁导率小 σ s
λ 0 (σ) = λ s , σ < 0. (7)
于铁镓的相对磁导率 (100) 时，随着相对磁导率的 2 ( 2σ )
降低，铁镓内部磁场强度急剧降低，且速度越来越 ln cosh
σ S
快；当相对磁导率降到 10 时，磁场强度是相对磁 Λ 0 (σ) = λ s σ s , σ < 0, (8)
4
导率为 100 时的一半；当降到与永磁体相对磁导率 其中，ε表示应变；M 为磁化强度；M s 为饱和磁化强
(1.2) 相同时，磁场强度为导磁件是铁镓时或电工纯 度；λ s 为饱和磁致伸缩应变系数；χ m 为初始磁化率；
铁时的 20%以下，具体如表 1 所示。由此可知，使用 σ s 为饱和预应力；µ 0 为真空磁导率；σ 为材料预应
永磁体提供偏置磁场时，因永磁体比铁镓的磁导率 力；E s 为饱和杨氏模量；L 为磁致伸缩材料磁化模
小得多，使得线圈提供的磁场绝大部分都耗散在永 型，目前模型函数有线性函数、双曲正切函数、朗之
磁体内部，严重影响了驱动效率。 万函数等，这里选择符合波尔兹曼统计的朗之万函
为了解决这个问题，考虑铁镓具有低场高磁致 数，表达式为
伸缩、近似线性区小的特点，提出一种无偏场非线 1
性驱动。当无偏场驱动时，磁路中不存在永磁体，相 L (x) = coth (x) − x . (9)
同驱动电流提供的磁场是有偏置时的 5 倍以上，极 从表达式可以看出，磁致伸缩方程分为两部分组成：
大地提高了驱动效率。 材料的磁化导致的磁致伸缩应变与磁致伸缩材料