Page 91 - 《应用声学》2023年第1期

第 42 卷 第 1 期 赵佳恒等： 铁镓 Janus-Helmholtz 换能器非线性驱动 87

的磁化方式，它们都和预应力有一定的关系。但在 反朗之万函数[3, 2]阶的帕德逼近可以写为
实际应用中，预应力是预先设定好的，是一个固定的 ( 9 297 ) ( )
2
L −1 (x) = x 3 + x + x 4 + O x 6
值σ 0 。从方程可知磁致伸缩的非线性主要体现在磁 5 175
( 2 )
化方式上，为了更方便得到磁场强度与磁致伸缩应 x a 0 + a 2 x ( )
= + O x 6 . (14)
变之间的关系，将式(5)、式(6)联立，可得 1 + b 2 x 2
[ ] 根据式(12)，经过运算得到帕德近似的参数a 0 、
M s −1 M 2 [λ s σ − Λ 0 (σ)]
H = L − M. (10) a 2 、b 2 ：
3χ m M s µ 0 M s 2
( )
36 2
400 x 3 − 35 x ( )
L −1 (x) = + O x 6 . (15)
33 x 2
1 −
ᇓᒱͩ᎖ऄԫ/10 -6 200 误差都在6%以下，对式(15)四舍五入取整：
300
35
为了得到更简捷的结果，考虑参数与各自取整
)
(
(
50 MPa
100 75 MPa L −1 (x) = x 3 − x 2 2 + O x 6 ) . (16)
25 MPa 1 − x
0 MPa 代表材料磁化过程的方程(10)可以写为
0 2 3
0 2 4 6 8 10 12 3MM − M 2 [λ s σ − Λ 0 (σ)]
s
H = − M. (17)
4
ᇓڤूए/(10 ASm -1 ) 2 2 2
3(χ M − M ) µ 0 M
m s s
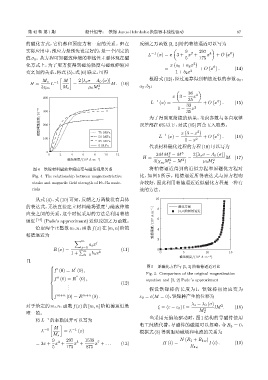
图 4 铁镓材料磁致伸缩应变与磁场强度关系 将帕德逼近得到的近似方程和原磁化方程对
Fig. 4 The relationship between magnetostrictive 比，如图 5 所示。帕德逼近所得表达式与原方程吻
strain and magnetic field strength of Fe-Ga mate- 合较好，因此利用帕德逼近近似磁化方程是一种有
rials 效的方法。
从式 (4)、式 (10) 可知，反朗之万函数没有具体 10
的表达式，无法直接建立材料磁场强度与磁致伸缩 8 ⻱ॆᯩ〻
应变之间的关系，这个时候采用的方法是利用帕德 [3,2]䱦ᑅᗧ䙬䘁
逼近 [14] (Pade’s approximant)近似反朗之万函数。 ᇓڤूए/(10 4 ASm -1 ) 6
给定两个正整数 m、n，函数 f(x) 在 [m, n] 阶的 4
帕德逼近为
∑ m j 2
a j x
j=0
R (x) = ∑ n (11) 0
1 + k=1 k x k 0 5 10 15
b
5
ᇓӑूए/(10 ASm -1 )
且
 图 5 原磁化方程与 [3, 2] 阶帕德逼近对比
′
f (0) = R (0) ,
 ′
 Fig. 5 Comparison of the original magnetization


 ′′
f (0) = R (0) ,
 ′′ equation and [3, 2] Pade’s approximant
. (12)
 . .
 假设铁镓棒的长度为 l，铁镓棒初始应变为




 m+n m+n ε 0 = ε(M = 0)，铁镓棒产生的位移为
f (0) = R (0) .
对于给定的 m、n，函数 f(x) 的 [m, n] 阶帕德逼近是 ξ = (ε − ε 0 ) l = λ s − λ 0 (σ) lM . (18)
2
M 2
唯一的。 s
当采用无偏场驱动时，图 1 结构的导磁件使用
将L −1 的泰勒展开可以写为
电工纯铁代替，导磁件的磁阻可以忽略，令R 2 = 0，
[ ]
M −1
−1
L = L (x) 根据式(3)得到驱动磁场和电流的关系为
M s
9 3 297 5 1539 7 N (R 1 + R 1w )
= 3x + x + x + x + . . . (13) H (t) = I (t) . (19)
5 175 875 R 1w