Page 207 - 《应用声学》2023年第2期

第 42 卷 第 2 期 张默涵等： 经颅超声刺激人脑海马的数值仿真研究 395

1.3 Pennes生物热传导方程 当超声的机械力作用在神经元的膜上时，电容
使用 Pennes 生物热传导方程 [20] 在数值仿真 模型的表达式 [24] 为
中描述温度场，探究靶区脑组织的温升，其表达式为 V (t) = (QA 1 /kε 0 KA 2 )p, (13)
∂T 2
ρC r = r ec ∇ T + q − W B C B T, (7) 式 (13) 中，Q 为穿过神经元细胞膜的电荷量；A 1 为
∂t
式(7)中，C r 为介质比热；T 为温度；r ec 为热传导率； 机械力作用于细胞膜的面积；A 2 为细胞膜表面积；k
1/f P 2 为弹性常数；ε 0 为自由空间的介电常数；K 为介电
∫
单位体积的发热量q = 2αI，声强I = f dt；
ρc 常数。
0
W B 为血流灌注量；C B 为血流比热。
1.4 机械指数 2 数值仿真模型及激励信号
MI计算式为 2.1 数值仿真模型及仿真参数

P PNP
MI = √ , (8) 基于 44岁健康男性志愿者CT数据和如图1 所
f
示人体脑内海马位置，建立如图 2 所示的三维经
式(8)中，P PNP 为峰值负压。
颅超声刺激海马的数值仿真模型，该模型由 128 阵
1.5 空间峰值时间平均声强 元相控换能器、人体头颅、水体构成。其中阵元
I spta 计算表达式 [21−22] 如下： 间等间距分布的相控阵换能器开口半径为 R、曲
率半径为 R z 、阵元直径为 2r。数值仿真模型区域
t 2 − t 1 p 2
Ispta = , (9) 为 140 mm×120 mm×120 mm，仿真的空间步长和
T 1 2ρc
时间步长分别设定为 dx = dy = dz = 0.25 mm，
式(9) 中，T 1 为脉冲重复周期，t 2 − t 1 为一个周期内
dt = 10 ns [18,25] 。水及皮质骨的声学仿真参数如
的脉宽，(t 2 − t 1 )/T 1 = DC为脉冲超声的占空比。
表 1 所示 [18,26−28] 。超声刺激海马神经元的电容模
1.6 电容模型方程 型中使用的仿真参数如表2所示 [24,29] 。除皮质骨外
基于 Izhikevich 神经元模型 [23] 的海马神经元 的非均质颅骨和脑组织在头部各空间位置的密度
放电行为表达式为 (ρ)、声速(c)和衰减系数(α)由式(3)∼(6)计算得出。
dv 2
= 0.04v + 5v + 140 − u + I 1 , (10)
dt
du
= a(bv − u), (11)
dt
其中，v 为膜电位；I 1 为外输入电流；a为时间尺度参
数；b 为依赖程度参数；u 用来代替生理模型中激活
的 K 离子电流和失活的 Na 离子电流，实现对膜电
位v 的负反馈；当膜电位v > 30 mV时，

v = c 1 ,

(12)
u = u + d,

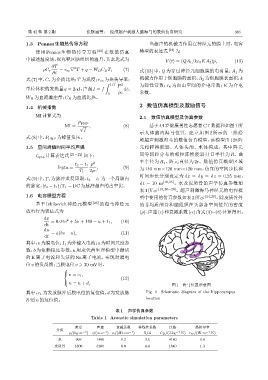
图 1 海马位置示意图
其中，c 1 为发放脉冲后膜电位的复位值，d 为发放脉 Fig. 1 Schematic diagram of the hippocampus
冲后u的复位值。 location

表 1 声学仿真参数
Table 1 Acoustic simulation parameters

密度 声速 衰减系数 非线性系数 比热 热传导率
介质
ρ/(kg·m −3 ) c/(m·s −1 ) α/(dB·cm −1 ) B/A C B /(J·kg −1 ·K) r ec/(W·m −1 ·K)
水 998 1486 0.2 3.5 4180 0.6
皮质骨 1600 3200 8.0 4.4 1840 1.3