Page 212 - 《应用声学》2023年第4期

874 2023 年 7 月

4
4
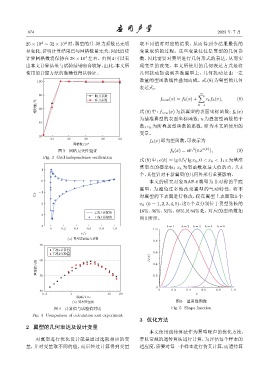
25 × 10 ∼ 32 × 10 时，翼型的升、阻力系数已无明 取不同值时对应的结果，从而得到令结果最优的
显变化，证明计算结果已与网格数量无关，因此后续 变量取值的过程。这些变量往往是翼型的几何参
4
计算网格数将保持在 28 × 10 左右。由图 4 可以看 数，因此需要对翼型进行几何形式的表达，从而实
出本文计算结果与试验结果吻合较好，由此，本文所 现变量的改变。本文所使用的几何表达方式是将
使用的计算方法的准确性得以验证。 几何扰动加载到基准翼型上，几何扰动是由一定
数量的型函数线性叠加而成。式 (8) 为翼型的几何
100
表达式。
n
80 ᫾ҧጇ஝ f new (x) = f 0 (x) + ∑ c k f k (x), (8)
Ӥҧጇ஝
ᄱࠫϙ/% 60 式 (8) 中：f new (x) 为新翼型的表面坐标函数；f 0 (x)
k=1
为基准翼型的表面坐标函数；n 为叠加型函数的个
40
数；c k 为所叠加型函数的系数，即为本文所使用的
变量。
20
24 26 28 30 32
f k (x)即为型函数，可表示为
Ꭺಫ஝/10 4
3
图 3 网格无关性验证 f k (x) = sin (πx e(k) ), (9)
Fig. 3 Grid independence verification
式 (9) 中：e(k) = lg 0.5/ lg x k , 0 < x k < 1；x 为基准
翼型点的横坐标；x k 为型函数取最大值的点，共 k
1
个，其位置对于新翼型的几何外形有重要影响。
0 本文的研究对象 RAF-6 翼型为非对称的平底
翼型，为避免过多地改变翼型的气动特性，将不
-1
C P 对翼型的下表面进行修改，仅在翼型上表面取 5 个
-2 x k (k = 1, 2, 3, 4, 5)，这 5 个点分别位于翼型弦长的
16%、36%、52%、68% 及 84% 处，对应的型函数如
ࢺц1ᝠካϙ
-3
ࢺц1តᰎϙ 图 5所示。
-4 k/ k/ k/ k/ k/
0 0.2 0.4 0.6 0.8 1.0 1.0
x⊳c
(a) Ꮳی᛫᭧ԍҧጇ஝
0.8
70
ࢺц2ᝠካϙ
ࢺц2ࠄᰎϙ ƒ k↼x↽ 0.6
60
ܦԍጟ/dB 50 0.4

0.2

0
40 0 0.2 0.4 0.6 0.8 1.0
0.2 1 10 20 x
ᮠဋ/kHz
(b) Ꮳیܦԍጟ 图 5 型函数图像
图 4 计算值与试验值对比 Fig. 5 Shape function
Fig. 4 Comparison of calculation and experiment
3 优化方法
2 翼型的几何表达及设计变量
本文使用遗传算法作为翼型噪声的优化方法，
对翼型进行优化设计就是通过选取相应的变 若以常规的遗传算法进行计算，为评估每个样本的
量，并对变量取不同的值，而后经过计算得到变量 适应度，需要对每一个样本进行仿真计算，而遗传算