Page 225 - 《应用声学》2024年第1期

第 43 卷 第 1 期 孔惠元等： 圆柱类构件超声相控阵聚焦模型 221

3.3 楔块耦合仿真验证 表 6 两种算法计算结果对比
将耦合剂换为有机玻璃制楔块，由于偏转聚 Table 6 Comparison of the calculation re-
焦情况更为普遍，对于只聚焦的情况这里不再阐 sults of the two algorithms
述。将聚焦点设于换能器中心位置右侧4 mm、深度 计算方法 费马定律 本文方法
10 mm，根据上述原理得各阵元延迟时间，同时对本 离散精度/mm 0.01 0.01
文方法与费马定律算法分别进行编程，对比结果如 迭代次数 6500 294
表6所示。 耗时/s 0.75 0.22
由表 6 可知本文方法迭代次数较少，且计算效
率有效提高，对各阵元进行计算所得参数如表 7 由焦点坐标可得聚焦点位于换能器中心位置
所示。 右侧向深度方向偏转 68 ，绘制该方向声压分布，如
◦
将表 7中的延时数据加到换能器各阵元仿真声 图11所示(数据经过归一化处理)，在10 mm深度左
场分布，如图 10 所示。图 10(a) 所有换能器各阵元 右声压值达到最大，之后随着深度增加声压减小，与
按照表 7 的延时依次激发超声波，图 10(b) 表示在 预期结果基本吻合。此外计算了其他聚焦点的延时
3.9 µs 左右所有阵元辐射超声波在预设焦点实现 法则并进行声场仿真验证，与上述聚焦结果类似，声
聚焦。 束都可以在指定位置实现聚焦。

表 7 各阵元编号、有机玻璃中声程、被测构件中声程和延迟时间
Table 7 The number of each array, the plexiglass middle sound path,
the measured component middle sound path and the delay time

阵元编号 l 1 /mm l 2 /mm ∆T/µs 阵元编号 l 1 /mm l 2 /mm ∆T/µs
1 5.3975 8.2770 0 9 5.1216 5.6643 0.5363
2 5.3500 7.8624 0.0798 10 5.0898 5.4704 0.5809
3 5.3218 7.4691 0.1568 11 5.0612 5.3059 0.6187

4 5.2914 7.0991 0.2307 12 5.0371 5.1820 0.6492
5 5.2590 6.7544 0.3011 13 5.0183 5.0881 0.6720
6 5.2251 6.4371 0.3676 14 5.0059 5.0279 0.6868
7 5.1903 6.1487 0.4290 15 5.0003 5.0014 0.6933
8 5.0453 5.8907 0.4855 16 5.0018 5.0086 0.6915

0 0
-4 -4
ጫՔͯረ/mm -12 ጫՔͯረ/mm -12
-8
-8

-16 -16
-20 -20
-15 -10 -5 0 5 10 15 -15 -10 -5 0 5 10 15
ഷՔͯረ/mm ഷՔͯረ/mm
(a) 2 µs (b) 3.9 µs
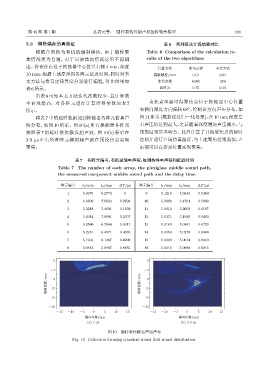
图 10 偏转聚焦瞬态声场声布
Fig. 10 Deflection focusing transient sound field sound distribution