Page 32 - 《应用声学》2024年第1期

28 2024 年 1 月


 w 1 PSLL(r 1 , r 2 , · · · , r 192 ) + [w 2 PSLL(r 1 , r 2 , · · · , r 64 )





 + w 3 PSLL(r 1 , r 3 , r 5 , · · · , r 63 , r 64 , · · · , r 128 )
′
Fitness = (8)
 + w 4 PSLL(r 1 , r 5 , · · · , r 61 , r 65 , r 67 , · · · , r 127 , r 129 , r 130 , · · · , r 192 )],





r 1 , r 2 , r 3 , · · · , r n > 0, r 1 = 0, r 192 = 222.

最后设置终止条件为：(1) 适应度函数值小于 数能够越早的收敛，但存在最优适应度值和平均适
设定目标值−60 dB。(2) 迭代代数超过500。(3) 超 应度值差距较大问题，反映出子代个体的差异性很
过50代的适应度函数值未下降。满足以上3个条件 大，不够稳健 (图 6 所示)。相较于优化前，优化后适
之一则程序终止，输出最优解。经过多次实验，得到 应性函数可以在较低的运算量基础上表现更为稳
两种适应性函数的子代平均适应度值和最优适应 健，且最终收敛值 (图 7 所示) 与图 6 所示收敛值一
度值变化如图6和图7所示。 致。优化后的适应性函数的平均适应度值在 300 代
之后存在起伏现象，该现象是大种群数量下子代多
-40
样性的体现，在多次迭代平均适应度值未变化时，种
ࣱکᤠऄएϙ
-45 త͖ᤠऄएϙ 群就会试图采取变异破坏这种平衡去扩大搜索范
围，最终都会在收敛值上浮动，且最优适应度值达到
ᤠऄएϙ/dB -50 收敛不变。该结果直观验证了采用遗传算法对上述

-55
阵型进行优化，终止原则难以准确确定，但通过基于
概率搜索，具有摆脱局部最优的能力，得到全局最
-60
优解。
-65 在相同的效果下，选取优化后的式 (8) 适应度
0 50 100 150 200 250 300 350 400 450 500
ᤖ̽ߕ̽஝ 函数进行阵型优化，该函数相比式 (7) 函数能够大
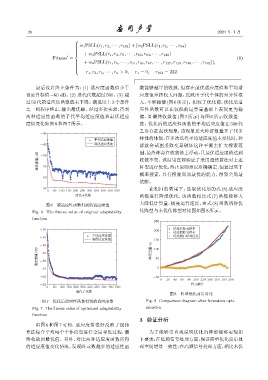
图 6 原适应性函数得到的适应度值 大降低计算量，提高运算速度，由式 (8) 函数所得优
Fig. 6 The fitness value of original adaptability 化阵型与未优化阵型对比图如图8所示。
function
250
-30 200 ͖ӑՑ᫼Ћଆ࣋
͖ӑҒ᫼Ћଆ࣋
ࣱکᤠऄएϙ ͖ӑҒՑᄱࠫͯᎶ
-35
త͖ᤠऄएϙ 150
-40 100
ᤠऄएϙ/dB -45 ᫼ЋͯᎶ/m 50

-50
-55 0
-60 -50
0 20 40 60 80 100 120 140 160 180 200
-65 ᫼ЋᎄՂ
0 50 100 150 200 250 300 350 400 450 500
ᤖ̽ߕ̽஝
图 8 阵型优化前后对比
图 7 优化后适应性函数得到的适应度值 Fig. 8 Comparison diagram after formation opti-
Fig. 7 The fitness value of optimized adaptability mization
function
3 验证分析
由图 6 和图 7 可知，适应度值很好反映了遗传
算法综合平均每个个体信息进行全局寻优过程，最 为了能够更直观说明优化后阵型能够实现如
终收敛到最优值。另外，对比两种适应度函数所得 下要求：在低频信号处理方面，保证阵型优化前后处
的适应度值变化情况，发现阵元数越多的适应性函 理空间增益一致性；在高频信号处理方面，相比未优