Page 9 - 《应用声学》2024年第1期

第 43 卷 第 1 期 沈鑫玉等： 遗传算法优化变分模态分解提取舰船辐射噪声特征线谱方法 5

2.3.2 理论分析 由式 (20) 可以看出，线谱输出增益 G 与信号
接下来，对 GA-VMD 降噪算法抑制噪声的性 主导分量占全部分量的比例 M/K 呈负相关，即
能进行理论分析。从降噪后信号的 SNR 以及谱分 M/K 越小，线谱输出增益 G越大。由于 VMD 的准
析后的线谱输出增益两方面进行分析。 确性越高，信号的频段划分就越精细，模态分量总
由于适应度函数保证了优化方向朝着输出 数越大，所以在信号主导分量阶数 M 一定的条件
SNR 最高的方向进行，所以在一定程度上保证了 下，GA-VMD后的M/K 更小。由此可以看出，基于
GA-VMD降噪算法在 SNR上的优越性。GA-VMD GA-VMD 的降噪方法提取出的线谱输出增益更大，
算法的降噪效果通过均方误差(Mean square error, 对噪声的抑制能力更强。
MSE)和输出SNR评价，计算公式为
3 仿真实验
[ ] 1/2
N
∑ 2
′
MSE = (s(i) − s (i)) /N , (15) 根据上述仿真信号模型，设置舰船螺旋桨叶片
i=1
  数为 4，轴频为 50 Hz，加入某次实测的海洋环境噪
∑ N 2
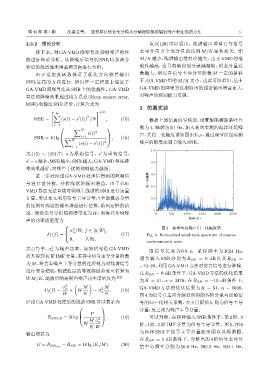
s(i) 声，其归一化幅度谱如图 3所示，通过调节所加实测
i=1
  (16)
SNR = 10 lg  ∑ N 2  , 噪声的幅度来调节输入SNR。
′
(s(i) − s (i))
i=1
1.0
式 (15) ∼ (16) 中，s 为原始信号，s 为重构信号，
′
s − s越小，MSE越小，SNR越大，GA-VMD算法降 0.8
′
噪效果越好，对噪声干扰的抑制能力越强。
进一步对经过 GA-VMD 处理后得到的降噪信 0.6
号进行谱分析，分析线谱的输出增益。由于 GA- ॆʷӑࣨए 0.4
VMD算法无法直接对频域上线谱的SNR进行定量
计算，所以本文利用信号主导分量占全部模态分量 0.2
的比例对线谱的输出增益进行估算，给出定性的结
0
论。假设信号分析的频谱带宽为 W，则海洋环境噪 0 500 1000 1500 2000 2500
声的功率谱密度为 ᮠဋ/Hz
 海洋环境噪声归一化幅度谱
σ /W, f ∈ [0, W],
 2 图 3
n
P 1 (f) = (17) Fig. 3 Normalized amplitude spectrum of marine
0, 其他,

environmental noise
2
式 (17) 中，σ 为噪声功率。原始信号经 GA-VMD
n 取信号长度为 0.8 s， 采样频率为 1024 Hz，
后共得到K 阶IMF分量，若其中信号主导分量阶数
调节输入 SNR 分别为 R SN = 0 dB 以及 R SN =
为M，将舍弃噪声主导分量的过程视为对线谱信号
−10 dB，利用GA-VMD方法对仿真信号进行降噪。
进行窄带滤波，则滤波后的等效频谱带宽可估算为 在R SN = 0 dB条件下，GA-VMD方法的优化结果
WM/K，滤波后的高斯白噪声功率谱密度为 [21]
为 K = 41，α = 3476；在 R SN = −10 dB 条件下，
σ 2 n ( M ) 2 M GA-VMD 方法的优化结果为 K = 54，α = 5038。
P 2 (f) = × W = σ n . (18)
W K K 图 4 为信号自适应分解后所得的各阶分量与原始信
经过GA-VMD处理后的线谱SNR可以表示为 号的归一化相关系数，大于门限值 h 则为信号主导
 
分量，反之则为噪声主导分量。
P
  (19) 可以判断，在两种输入 SNR 条件下，第 2 阶、3
R SNout = 10 lg  2  .
M σ n
W 阶、4 阶、5 阶 IMF 分量为信号主导分量。图 5、图 6
K W
为两种 SNR 下信号主导分量波形图以及频谱图。
输出增益为
在 R SN = 0 dB 条件下，分解出的 4 阶信号主导分
− R SN = 10 lg (K/M) . (20)
量中心频率分别为 50.0 Hz、200.2 Hz、100.1 Hz、
G = R SN out