Page 224 - 《应用声学》2024年第6期

1400 2024 年 11 月

1200±5，而循环互相关法的波动值能达到 −50；由 综上所述，经改进后的互相关法优于循环互相
图3 可见，改进后的互相关法计算时延，相对误差平 关法，不仅运算量少，而且能更准确、稳定地测得时
均在 0.5% 以内；而循环互相关法在相同工况下，相 延估计值，因此，本文用该方法进行仿真模拟进行时
对误差高达 13%。进一步计算平均相对误差，改进 延估计是准确可行的。
后的互相关法平均误差仅为 0.17%；而循环互相关 2.3 声信号选择
法为3.3%。
以单路径回声法测温为研究对象，鉴于前人在
表 1 不同采样频率下两种算法的时延估计误差
双传感器测温实验的经验，线性扫频信号在测温中
Table 1 Time delay estimation error of
有较好的效果 [16] ，其表达式为
the two algorithms at different sampling
f(τ g ) − f 0
frequencies f(τ) = f 0 + τ, τ ∈ [0, τ g ], (14)
τ g
采样 循环互相关算法 一次互相关算法 式 (14) 中，f 0 为 0 时刻扫频信号的瞬时频率；f(τ g )
频率/kHz 均方根 平均相对 均方根 平均相对 为 τ g 时刻点扫频信号的瞬时频率；[0, τ g ] 为信号的
误差 误差/% 误差 误差/%
持续时间。因此，本文用 500∼8000 Hz 的扫频信号
25.6 197.21 4.95 4.27 0.34
作为激励信号，设定时延值为 1200，声衰减系数
38.4 103.09 3.40 3.06 0.22
为 0.2。在声源信号中加入高斯白噪声，信噪比从
51.2 80.92 3.65 2.84 0.21
15 dB 不断降低，研究扫频信号计算时延的稳定性。
64.0 67.52 3.43 2.79 0.20
102.4 66.20 3.30 2.59 0.17 结果表明，扫频脉冲信号的临界信噪比为 −10 dB，
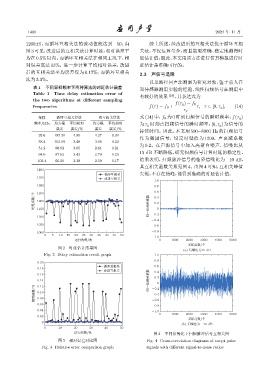
其互相关函数关系见图 4。由图 4可知，互相关峰值
1400
॰ဗ̉ᄱТ 尖锐，不存在伪峰，能得到准确的时延估计值。
1350 ஈᤉ̉ᄱТ
1.0
1300 0.8
0.6
௑णག஝/˔ 1200 ॆʷӑᄱТጇ஝ 0.4
1250
0.2
0
1150
1100 -0.2
-0.4
1050 -0.6
-0.8
1000
0 5 10 15 20 25 30 35 40 45 50
-1.0
ᤂᛡ൓஝/൓ 0 1000 2000 3000 4000 5000
᧔ನག஝/˔
图 2 时延估计结果图
(a) η٪උ˞15 dB
Fig. 2 Delay estimation result graph 1.0
0.8
0.20
॰ဗ̉ᄱТ 0.6
0.18
ஈᤉ̉ᄱТ 0.4
0.16
0.14 ॆʷӑᄱТጇ஝ 0.2 0
0.12
ᄱࠫឨࣀ/% 0.10 -0.2
-0.4
0.08
0.06 -0.6
-0.8
0.04 -1.0
0 1000 2000 3000 4000 5000
0.02
᧔ನག஝/˔
0
(b) η٪උ˞-10 dB
0 10 20 30 40 50
ᤂᛡ൓஝/൓ 图 4 不同信噪比下扫频脉冲信号互相关图
图 3 相对误差对比图 Fig. 4 Cross-correlation diagrams of swept pulse
Fig. 3 Relative error comparison graph signals with different signal-to-noise ratios