Page 225 - 《应用声学》2024年第6期

第 43 卷 第 6 期 余思琦等： 基于回声感知技术的介质温度监测 1401

此外，对 500∼8000 Hz 中脉宽为 50%的高斯脉 见，互相关峰值尖锐，能够得到准确的时延估
冲信号进行筛选，高斯脉冲信号的表达式为 计值。

2
2
f(τ) = A · e −(τ−τ 0 ) /(2σ ) , (15) 1.0
式 (15) 中，A 为振幅，τ 0 为高斯脉冲信号的中心时 0.8
0.6
间，σ 为标准差。仿真设定时延值为 1200，声衰减系
0.4
数为 0.2。由图 5 可知，1200 Hz 的高斯脉冲信号临 0.2
界信噪比最小，为−15 dB；由图 6 可知，1200 Hz 的 ॆʷӑᄱТጇ஝ 0
高斯脉冲信号在最低信噪比下模拟 50 次得到的平 -0.2
均时延估计值最准确为 1200，标准差为 1.63。因此， -0.4
选取频率为 1200 Hz、脉宽为 50% 的高斯脉冲信号 -0.6
作为激励信号。 -0.8
-1.0
-9 0 1000 2000 3000 4000 5000
᧔ನག஝/˔
-10
(a) η٪උ˞15 dB
-11 1.0
ηඋ٪/dB -12 0.8
0.6
-13
ॆʷӑᄱТጇ஝ 0
0.2
-14 0.4
-15 -0.2
-16 -0.4
1200 2400 3600 4800 6000 7200 8400
ᮠဋ/Hz -0.6
-0.8
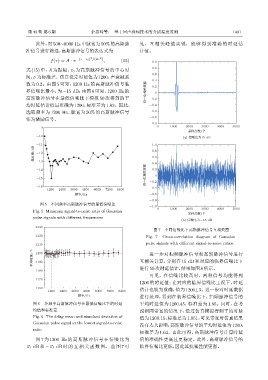
图 5 不同频率高斯脉冲信号的最低信噪比
-1.0
0 1000 2000 3000 4000 5000
Fig. 5 Minimum signal-to-noise ratio of Gaussian
᧔ನག஝/˔
pulse signals with different frequencies
(b) η٪උ˞-15 dB
1230
图 7 不同信噪比下高斯脉冲信号互相关图
1220 Fig. 7 Cross-correlation diagram of Gaussian
pulse signals with different signal-to-noise ratios
1210
ࣱک௑ण/˔ 1200 互相关计算，分别在 15 dB 和对应的临界信噪比下
进一步对扫频脉冲信号和高斯脉冲信号进行
1190
1180 进行50次时延估计，结果如图8所示。
可见，在信噪比较高时，两种信号均能得到
1170
1200 的时延值；在对应的临界信噪比工况下，时延
1160 估计也较为准确，值为 1200±3。进一步对时延数据
1200 2400 3600 4800 6000 7200 8400
ᮠဋ/Hz 进行处理，得到在临界信噪比下，扫频脉冲信号的
图 6 各频率高斯脉冲信号在最低信噪比下的时延 平均时延值为 1200.45，标准差为 1.85。同时，在考
均值和标准差 虑相同带宽的情况下，经过仿真模拟得到平均时延
Fig. 6 The delay mean and standard deviation of 值为1200.15，标准差为 1.851，可见带宽对仿真结果
Gaussian pulse signal at the lowest signal-to-noise
没有太大影响；高斯脉冲信号的平均时延值为1200，
ratio
标准差为 1.63。由此可得，高斯脉冲信号计算时延
图 7 为 1200 Hz 的高斯脉冲信号在信噪比为 值的准确性更高且更稳定。此外，高斯脉冲信号的
15 dB 和 −15 dB 时的互相关函数图。 由图 7 可 临界信噪比更低，因此其抗噪性能更强。