Page 233 - 《应用声学》2024年第6期

第 43 卷 第 6 期 曾广栋等： 大型螺栓阵列超声全聚焦成像的场能强化算法研究 1409

Y
其中，L Aa = 2 × S AOb m /R，S AOb m 为三角形AOb m
的面积。
ѭጳL 
A
ѭጳL  √
L ce = R − L 2 ′ − L 2 , (10)
O C Cc
其中，L Cc = 2 × S CO e /R，S CO e 为三角形CO e 的
′
α 
b  X ′ ′
O
面积。
β  α 
已知 = ，L B m b m = z B m ，L B m e =
β  b  L ab m L ce
L B m b m L B m e
，可推得
z C − z B m
c
√
( ) 2
R − L 2 − 2 × S AOb m
OA
z B m R
= √ . (11)
图 4 顶截面投影图 ( ) 2
z C − z B m
′
2 × S CO e
2
′ −
Fig. 4 Top section projection R − L O C R
= R，式(5)可表示为
又因为L Ob m 当 A 点、C 点和 b m 点的坐标已知时，式 (10) 中仅
2
2
L 2 + R − L 2 L 2 + R − L 2 ) 点
Ab m AO cb m cO (6) z B m 为未知量，以此可求得 B m (x B m , y B m , z B m
= ,
· R · R
2 · L Ab m 2 · L cb m 三维坐标。
2
2
其中，L 2 = (x A − x b m ) + (y A − y b m ) ，L 2 =
Ab m cb m
2 2 2 2 2 。 Z
(x c − x b m ) + (y c − y b m ) ，R = x + y Y
b m b m
A(x A , y A , z A ) 和 C(x C , y C , z C ) 点的坐标和螺
A X
栓 半 径 R 为 已 知 条 件； b m (x b , y b , z b ) 点 坐 标 中 O
a
z b = 0、b m (x b , y b , 0) 为未知量。第一步，将已知 b m
条件代入公式 (6) 则为二元二次方程，求方程的穷
B m
尽解得到 b m 点不唯一；在使用枚举法过程中，枚举
b m 点的步长应小于发射超声波的半波长。第二步，
, 0) 点集合，经过合理性筛选， Oϕ
由得到的 b m (x b m , y b m c
e
)点 C
再进一步计算出满足要求的B m (x B m , y B m , z B m
的值。
的Z 轴坐标z B m
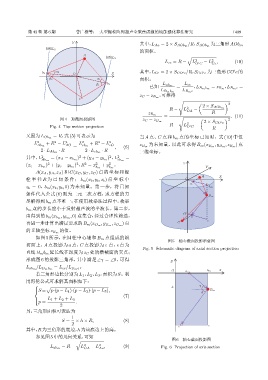
如图 5 所示，在圆柱中心轴和 B m 点组成的纵
图 5 轴心截面投影示意图
切面上，A 点投影为 a 点，C 点投影为 c 点，e 点为
Fig. 5 Schematic diagram of axial section projection
直线 B m b m 延长线在深度为 z C 处的横截面的交点；
形成图 6 的投影三角形，其中满足 ∠γ = ∠θ，可得
Z
= L ce /L B m e 。
L ab m /L B m b m
O a b m X
若三角形边长分别为 L 1 、L 2 、L 3 ，面积为 S。利
用海伦公式可求解其面积如下：
 γ
√ k
S = p·(p − L 1 )·(p − L 2 )·(p − L 3 ), θ B m

(7)
 L 1 + L 2 + L 3
 p = .
2
另，三角形面积可表达为
1
S = × h × R, (8)
2
c e
其中，R 为三角形的底边，h为该底边上的高。
参见图5中的几何关系，可知
图 6 轴心截面投影图
√
= R − L 2 − L 2 , (9)
OA Aa
L ab m Fig. 6 Projection of axis section