Page 136 - 《应用声学》2025年第1期

132 2025 年 1 月

心的位置设置为 0、m/2 和m，分别对应频谱图上有 随后对弱相关分量进行 WPT 处理，并将处
效信号带宽分布在前部、中部和后部的情况。在表 理后的弱相关分量与强相关分量重构，得到降噪
示上，使用SPIC-0、SPIC-0.5、SPIC-1区分。 信号。在此引入传统的 CEEMD 降噪算法作为对
由于计算SPIC所需的参数可直接由信号得到， 比，为了提升对比效果，传统的 CEEMD 降噪算法
所以可以用来量化真实信号的降噪效果，其真实的 采用与 CEEMD-WPT 相同的信号重构方法。分别
量化效果由第3节验证。 绘制两种降噪结果的波形图和频谱图，如图 6 所

示，对比观察可以发现两种方法均有较好的降噪
3 仿真分析
效果，但是传统 CEEMD 降噪结果的高频部分有噪
为了验证本文提出的 CEEMD-WPT降噪效果 声残留，而 CEEMD-WPT 高频部分的噪声残留较
和 SPIC 量化效果，在此引入 Mitrakovic 等 [21] 提出 少，低频部分未出现失真现象，具有更好的降噪
的 AE 信号数字模型进行仿真实验，该模型表达式 效果。
如式(15)所示：
5
I ե٪ηՂ
∑ 2 ԔηՂ
f(t) = F i e [−Q i (t−t i ) ] sin[2πf i (t − t i )], (15)
i=1
式(15) 中，F i 为第 i个信号的幅值，Q i 为第 i 个信号
的衰减因子，t i 为第 i 个信号的延迟时间，f i 为第 i ࣨϙ 0
个信号的频率，I 为叠加信号个数。
本文采用的模拟参数如表 1 所示，并用 Matlab
进行仿真模拟，采样点个数为 2000，采样频率为
1000 kHz，其波形和频谱图如图3中的红线所示。为 -5
0 500 1000 1500 2000
了模拟环境的噪声，在模拟信号上添加SNR为5 dB ᧔ನག/˔
的白噪声，含噪信号的波形图和频谱图如图 3 中的 (a) ฉॎڏ
蓝线所示。可以看出，噪声使得模拟信号波形出现 0.7
0.7 ե٪ηՂ
震荡现象，频域成分变得更加复杂，这将对信号的后
0.6 ԔηՂ
续识别造成不利影响。
0.5 ࣨϙ 0.6
表 1 模拟信号参数
Table 1 Analog signal parameters 0.4
ࣨϙ 0.5 7 8 9
0.3
ᮠဋ/kHz
参数 I D i Q i t i /s f i /kHz
0.2
数值 1 4 120 0.4 40
0.1
对图 3 中的含噪信号进行改进的 CEEMD，得
0
到 9 个 IMF 分量和 1 个 RES，然后对其进行傅里叶 0 50 100 150 200
ᮠဋ/kHz
变换获得对应的频谱图，其结果如图4所示。然后依
(b) ᮠ៨ڏ
次计算 IMF 分量与含噪信号的互相关系数，如图 5
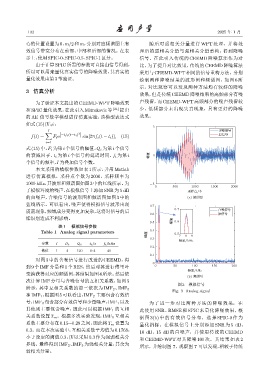
图 3 模拟信号
所示，其中互相关系数的前三依次为 IMF 2 、IMF 3
Fig. 3 Analog signal
和IMF 1 ，根据图5可以看出，IMF 2 主要包含有效信
号，IMF 3 包含部分有效信号和少量噪声，IMF 1 以及 为了进一步对比两种方法的降噪效果，在
其他则主要包含噪声，因此可以根据 IMF 1 的互相 此使用 SNR、RMSE 和 SPIC 来量化降噪效果，根
关系数设置 T m 。根据多次实验发现，IMF 1 互相关 据图 3(b) 中的有效信号分布，选择 SPIC-0 作为
系数主要分布在 0.15∼0.28 之间，因此将 T m 设置为 量化指标。在模拟信号上分别添加 SNR 为 5 dB、
0.3。而在本次实验中，互相关系数平均值为 0.1768， 10 dB、15 dB 的白噪声，并使用传统的 CEEMD
小于设定的阈值 0.3，所以采用 0.3 作为强弱相关分
和 CEEMD-WPT 对其降噪 100 次。其结果如表 2
界线。最终得到IMF 2 、IMF 3 为强相关分量，其余为
所示，并绘制图 7。观察图 7 可以发现，相较于传统
弱相关分量。