Page 156 - 《应用声学》2025年第1期

152 2025 年 1 月

2.2 有限元仿真及结果分析 f n = f 0 (1 + n) 1/2 的关系，其中，n 为谐振频率的阶
2.2.1 有限元仿真流程 数，f 0 为压电圆管换能器非相控激励时的径向谐振
使用有限元仿真软件对相控型圆管换能器进 频率，n = 1 时对应的是以偶极模态振动时圆管换
行仿真分析，主要仿真流程为：(1) 几何建模；(2) 添 能器的谐振频率。因此，理论上，相控激励时压电圆
√
加材料；(3) 选择合适的物理场；(4) 定义边界和初 管的谐振频率为同相激励的 2倍，仿真结果与理论
始条件；(5) 创建有限元网格；(6) 求解物理场；(7) 存在一定偏差。
生成所需可视化结果。
2.0
2.2.2 仿真结果分析

在施加不同的激励电压时，该压电圆管可以产 1.5
生同心圆声场以及螺旋声场，当对圆管的四部分施
加相同的激励电压时，可以产生同心圆声场；当对 ႃ࠮ጪ/mS 1.0 ႃ࠮జጳ
圆管的四部分施加如图2 所示不同相位的激励电压 ႃጪజጳ
0.5
时，可以产生螺旋声场。在有限元仿真软件中进行
仿真，可以分别得到同心圆声场以及螺旋声场声压
0
的可视化结果，如图6所示。 8 12 ᮠဋ/kHz 16 20
(a) ᭤ᄱ଍ړኮ૱ᑟ٨࠮ጪజጳ

2.5
ႃ࠮జጳ
ႃጪజጳ
2.0
ႃ࠮ጪ/mS
y y 1.5

z x z x 1.0
(a) x-yࣱ᭧Տॷړܦڤ (b) x-yࣱ᭧ᛃ஽ܦڤ 0.5

图 6 不同声压激励方式产生的同心圆声场以及螺旋声
0
场对比 10 20 30
ᮠဋ/kHz
Fig. 6 Comparison of concentric circle sound field
(b) ᄱ଍یړኮ૱ᑟ٨࠮ጪజጳ
and spiral sound field produced by different sound
pressure excitation modes
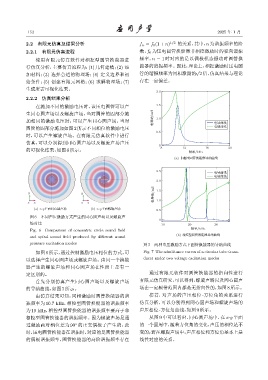
图 7 两种电压激励方式下圆管换能器的导纳曲线
如图 6所示，通过控制激励电压相位的方式，可 Fig. 7 The admittance curves of a circular tube trans-
以选择产生同心圆声场或螺旋声场。由同一个换能 ducer under two voltage excitation modes
器产生的螺旋声场和同心圆声场在性质上是有一
定区别的。 通过有限元软件对圆管换能器的指向性进行
首先分别仿真产生同心圆声场以及螺旋声场 有限元仿真研究，可以得到，螺旋声场以及同心圆声
的导纳曲线，如图7所示。 场在一定频带范围内都是无指向性的，如图8所示。
由仿真结果可知，同相激励时圆管换能器的谐 接着，对声场的声压相位 -方位角的关系进行
振频率为 10.7 kHz，相控型圆管换能器的谐振频率 仿真分析，可以分别得到同心圆声场和螺旋声场的
为19 kHz，相控型圆管换能器的谐振频率要高于非 声压相位-方位角曲线，如图9所示。
相控型圆管换能器的谐振频率。因为螺旋声场是通 从图 9 中可以看出，同心圆声场中，在 x-y 平面
过激励两对相位差为 90 的正交偶极子产生的，此 的一个圆周中，随着方位角的变化，声压的相位是不
◦
时，压电圆管换能器在谐振时，对应的是圆管换能器 变的；而在螺旋声场中，声压相位和方位角基本上是
的偶极谐振频率，圆管换能器的高阶谐振频率存在 线性对应的关系。