Page 251 - 《应用声学》2025年第1期

第 44 卷 第 1 期 龙士国等： 基于 LabVIEW 的智能建筑外墙饰面砖脱空识别软件开发 247

反射现象，进而使得信号传播距离延长，产生更多的 假设，利用均值 µ 和标准差 σ 来估计基本分布 [17] 。
能量损耗，导致接收到的信号首波幅值减小 [12] 。 采用拉依达准则筛选并剔除异常值，是为了避免异
常值对数据训练分类带来的影响。根据拉依达准
1.0 ళᑲቇ฾ག
则，认为在正态分布中，大约有99.7%的数据会落在
0.5 (µ − 3σ, µ + 3σ)范围内。当某个数据点的值与样本
均值相差超过3σ 时，就将其视为异常值 [18] 。
0
100 0.8
Y/֓⊲
ॆʷӑࣨएηՂ 1.0 ᑲቇ฾ག 80 0.7
-0.5
0.6
0.5
ࡇए 60 0.5
0.4
0
40 0.3
Y/֓⊲
-0.5 0.2
20
5 10 0.1
௑ᫎ/ms
0
0 2 4 6 8 10
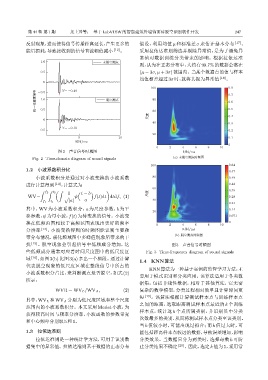
图 2 声音信号时域图 ௑ᫎ/ms
Fig. 2 Time-domain diagram of sound signals (a) ళᑲቇ฾ག௑ᮠڏ
100 0.64
1.2 小波系数积分比 0.57

小波系数积分是通过对小波变换的小波系数 80 0.49
进行计算得到 [13] ，计算式为 0.42
60
∫ ∫ (∫ ) 0.35
f 2 t 2 1 ( t − b ) ࡇए
WV= √ ψ f(t)dt dtdf, (1) 0.28
|a| a 40
f 1 t 1
0.21
其中，WV 为小波系数积分，a 为尺度参数，b 为平 0.14
20
移参数，ψ 为母小波，f(t) 为待变换的信号。小波变 0.071
换在低频范围相较于高频范围表现出更好的频率 0 2 4 6 8 10 0
分辨率 [14] ，小波变换得到的时频图能识别主要频 ௑ᫎ/ms
带分布情况，弱化频域图中多峰值现象所带来的干 (b) ᑲቇ฾ག௑ᮠڏ
扰 [15] 。脱空现象会引起信号中低频成分增加，这 图 3 声音信号时频图
些低频成分通常对应着时间尺度图中的低尺度区 Fig. 3 Time-frequency diagram of sound signals
域 [16] ，如图3(b)比图3(a)多出一个频段。通过计算
1.4 KNN算法
代表脱空现象的低尺度区域在整段信号中所占的
KNN算法为一种基于实例的监督学习方法，主
小波系数积分占比，来判断测点是否脱空，如式 (2)
要用于模式识别和分类应用。该算法适用于各类数
所示：
据集，包括非线性数据，相对于其他算法，它无需
WVR = WV L /WV A , (2) 复杂的数学模型，分类过程相对简单且计算时间更
短 [19] 。该算法根据计算测试样本点与训练样本点
其中，WV L 和WV A 分别为低尺度区域和整个尺度
之间的距离，选取距离测试样本点最近的 k 个训练
范围内的小波系数积分。本文采用 Morlet 小波，为
样本点，统计这 k 个点所属类别，并识别其中分类
获得较高时间与频率分辨率，小波函数的参数带宽
次数最多的类别，从而将测试样本点分类至该类别。
和中心频率分别取5和1。
当 k 值较小时，可能出现过拟合；而 k 值过大时，可
1.3 拉依达准则 能包括距离样本点较远的数据，导致误差增加，影响
拉依达准则是一种统计学方法，可用于识别数 分类效果。当数据只分为两类时，选择奇数 k 可防
据集中的异常值。拉依达准则基于数据的正态分布 止分类结果不确定 [20] 。因此，选定 k 值为5，采用常