Page 250 - 《应用声学》2025年第2期

510 2025 年 3 月

0.03 将提取的各齿的 AE 信号进行小波包分解，选
取正则性较好的 db4 小波基函数，并对各频段小波
0.02
ࣨϙ 系数求其 RMS 得到磨削过程频域特征。如图 5 所
0.01
示，进行各齿磨削 AE 信号的 3 层小波包分解能够
0 有效表征损伤特征。磨削 AE 信号能量主要集中在
0 50 100 150 200
ᮠဋ/kHz 低频的第 1 节点，随着磨削次数的增加，第 1 节点第
(a) Ғరᇜ૯AEᮠ៨ 2次磨削RMS最低，然后逐渐增大至稳定状态。
0.03
3 基于SVM的插刀磨砂轮识别模型
0.02
ࣨϙ
0.01 3.1 SVM
SVM 是以在数据模型中寻找最优超平面为目
0
0 50 100 150 200
ᮠဋ/kHz 标，最大化边际为核心思想的非线性二分类模型，通
(b) ˑ᧘ᇜ૯AEᮠ៨ 过核函数将低维特征映射在高维空间，实现非线性
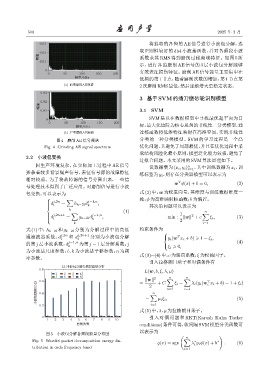
图 4 磨削 AE 信号频谱 分类的一种分类模型。SVM 的学习过程是一个凸
Fig. 4 Grinding AE signal spectrum 优化问题，其避免了局部最优，并且在优化过程中采
取结构风险化最小原则，模型泛化能力较强，避免了
2.2 小波包变换
过拟合问题。本文采用的SVM算法原理如下。
因生产环境复杂，在实际加工过程中 AE 信号 n
设数据集为 (x i , y i ) i=1 ，其中训练数据为 x i ，训
掺杂着较多背景噪声信号，表征信号源的故障特征 练标签为y i ，则存在分类器模型可以表示为
相对较弱。为了将故障源的信号分离出来，一些信
T
w ϕ(x) + b = 0, (2)
号处理技术得到了广泛应用。对磨削信号进行小波
包变换，可以表示为 式 (2) 中，w 为权重向量，其维度与训练数据维度一
 致；ϕ为高维映射核函数；b为偏置。
∑
 j,2n = h k−2l d j−1,n ,
d
 l k 其决策问题可以表示为

k (1)
n
∑ 1 ∑
 j,2n+1 j−1,n 2
d = g k−2l d , min : ∥w∥ + c ξ i , (3)

 l k 2
k i=1
式 (1) 中：h k−2l 和 g k−2l 分别为分解过程中的高低 约束条件为

j,2n j,2n+1
通滤波器系数；d 和 d 分别为小波包分解  T
l l y i (w x i + b) > 1 − ξ i ,
j−1,n (4)
的第 j 层小波系数，d 为第 j − 1 层分解系数；j
k  ξ i > 0,
为小波基尺度参数，l、k 为小波基平移参数；n 为频
式(3)∼(4)中，c为惩罚系数，ξ 为松弛因子。
率参数。
引入拉格朗日乘子和对偶条件有
3ࡏ࠵ฉӊѬᝍՊᮠ඀ᑟ᧚Ѭ࣋
0.8
1 2 3 4 L(w, b, ξ, λ, µ)
5 6 7 8 = ∥w∥ 2 + C ∑ ξ i − ∑ λ i (y i (w x i + b) − 1 + ξ i )
n
n
T
0.6
࠵ฉӊᮠ඀RMS 0.4 2 ∑ µ i ξ i , n=1 i=1 (5)
i
n
0.2 − i=1
式(5)中，λ、µ为拉格朗日乘子。
0 引入对偶问题和 KKT(Karush–Kuhn–Tucker
1 2 3 4 5 6 7 8 9 10
ᇜҐ൓஝ conditions)条件可得，软间隔SVM模型分类函数可
以表示为
图 5 小波包分解各频段能量分布图
( )
n
Fig. 5 Wavelet packet decomposition energy dis- ∑
g(x) = sgn λ y i ϕ(x) + b ∗ . (6)
∗
i
tribution in each frequency band
i=1