Page 261 - 《应用声学》2025年第2期

第 44 卷 第 2 期 杨斌等： 用于电磁超声检测信号的联合降噪方法 521

其中，y(t)为含噪信号，x(t)为目标纯净信号，e(t)为 随 VMD 分解层级的增加会快速衰减，可以通过引
噪声信号。 入功率Q进一步区分噪声与纯净信号。因此提出了
信号y(t)经离散WT后表达式为 IMF 选择评价系数 K w 用以筛选关键 IMF 分量，其

∞ 表达式为
∑

 y(t) = c k φ(t − k)


 r
 K w = sign (C) |C| Q, (11)
 k=−∞

∞ ∞
∑ ∑ (8) N
j
+ d j,k Ψ(2 t − k), 1 ∑
 2
 Q = x (i), (12)

 k=−∞ j=0
 N
 i=1

c k =⟨y(t), φ j,k (t)⟩, d j,k =⟨y(t), Ψ j,k (t)⟩,

其中，sign 为符号函数，指数 r 通常取 1，x(i) 为各
其中，φ为尺度函数，其作用相当于一个低通滤波器
IMF分量数据点，N 为IMF数据长度。
获取信号的近似部分；Ψ 为小波基函数，其作用相当
使用 K w 对 IMF 分量进行选择，在保证重构信
于一个高通滤波器获取信号的细节部分；c k 为信号
号与原始信号的相似性的同时也能通过对信号能
近似部分系数，d j,k 为信号细节部分系数，k 是控制
量的计算确保关键IMF分量选择的准确性。
小波基时间平移的时域参数，j 是控制小波基频率
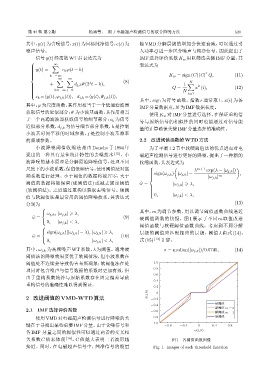
的频域参数。 2.2 改进阈值函数的WTD方法
小波降噪阈值收缩法是由 Donoho 于 1994 年 为了平衡 1.2 节中软硬阈值法的优点进而对电
提出的一种具有最佳统计特性的去噪技术 [15] 。小 磁超声检测信号进行更好的降噪，提出了一种新的
波降噪的基本原理是分解原始降噪信号，处理不同 收缩函数，其表达式为
尺度下的小波系数，保留低频信号，使用阈值法对高  ( m+1 )
 λ exp(λ − |ω j,k |)

频系数进行处理。小于阈值的数据将被置零，大于  sign(ω j,k ) |ω j,k | − m ,


 |ω j,k |
阈值的数据将被保留 (硬阈值法) 或减去固定阈值 ˆ ω = |ω j,k | > λ,

(软阈值法)。之后通过重构以获取去噪信号。硬阈 



 0, |ω j,k | < λ,
值与软阈值法是最常用的阈值降噪技术，其表达式
分别为 (13)

其中，m 为调节参数，用以调节阈值函数曲线逼近
ω j,k , |ω j,k | > λ,

ˆ ω = (9) 硬阈值函数的快慢。图 1 展示了不同 m 取值改进
0, |ω j,k | < λ,

阈值函数与软硬阈值函数曲线。考虑到不同分解

sign(ω j,k )(|ω j,k | − λ), |ω j,k | > λ, 层级的阈值应匹配相应的层级，阈值 λ 由式 (14)、

ˆ ω = (10)
0, |ω j,k | < λ,
 式 (15) [12] 计算：
其中，ω j,k 为高频噪声 WT 系数，λ 为阈值。通常硬 σ = median(|ω j,k |)/0.6745, (14)
阈值法的降噪效果要优于软阈值法，但小波系数在
阈值处不连续会导致伪吉布斯现象；软阈值法在处 1.0
理同时包含噪声与信号数据的系数时更加有效，但 0.8
0.6
由于重构系数始终与原始系数存在固定偏差导致
0.4
重构信号的准确性难以得到保证。
0.2
ω↼j֒k↽ 0
2 改进阈值的VMD-WTD算法 ⊥ -0.2
ᆶ᫠ϙ
-0.4
2.1 IMF选择评价系数 -0.6 ழ᫠ϙ m/
ழ᫠ϙ m/
使用 VMD 对电磁超声检测信号进行降噪的关 -0.8 ᣄ᫠ϙ
键在于寻找出某些重要IMF分量。由于含噪信号和 -1.0 -0.8 -0.4 0 0.4 0.8
ω↼j֒k↽
各 IMF 分量之间的相似性可以通过两者的交叉相
关系数 C 值来体现 [16] ，C 值越大表明二者波形越 图 1 各阈值函数图像
接近。同时，在电磁超声信号中，纯净信号的能量 Fig. 1 Images of each threshold function