Page 132 - 《应用声学》2025年第3期

666 2025 年 5 月

ԔݽηՂ ԔݽηՂ
0 0
160 140
ᮠ۫/Hz 120 -10 ᮠ۫/Hz 160 -10
140
120
100
100
80 -20 80 -20
5 10 15 20 25 30 35 40 45 50 55 5 10 15 20 25 30 35 40 45 50 55
௑ᫎ/s ௑ᫎ/s
CBF CBF
0 0
ᮠ۫/Hz 160 -10 ᮠ۫/Hz 160 -10
140
140
120
120
100
80
80 -20 100 -20
5 10 15 20 25 30 35 40 45 50 55 5 10 15 20 25 30 35 40 45 50 55
௑ᫎ/s ௑ᫎ/s
CBF-ALE CBF-ALE
0 0
ᮠ۫/Hz 160 -10 ᮠ۫/Hz 160 -10
140
140
120
120
100
80
80 -20 100 -20
5 10 15 20 25 30 35 40 45 50 55 5 10 15 20 25 30 35 40 45 50 55
௑ᫎ/s ௑ᫎ/s
CBF-FALE CBF-FALE
0 0
ᮠ۫/Hz 160 -10 ᮠ۫/Hz 160 -10
140
140
120
120
100
80 -20 100 -20
80
5 10 15 20 25 30 35 40 45 50 55 5 10 15 20 25 30 35 40 45 50 55
௑ᫎ/s ௑ᫎ/s
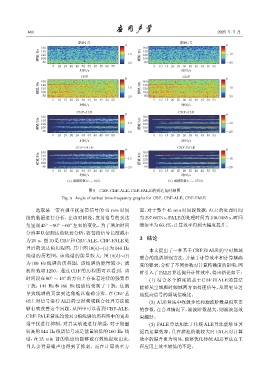
(a) ໚ฉ᫽஝(L=625) (b) ໚ฉ᫽஝(L=3750)
图 9 CBF、CBF-ALE、CBF-FALE 的到达角时频图
Fig. 9 Angle of arrival time-frequency graphs for CBF, CBF-ALE, CBF-FALE
选取某一带有强干扰宽带信号的 45 min 时间 面，对于整个 45 min 时间段数据，ALE 的处理时间
段的数据进行分析，在该时间段，发射信号的到达 为297.6073 s，FALE的处理时间为100.0385 s，时间
角呈现 45 −90 −60 左右的变化。为了增加时间 缩短率为66.4%，计算效率得到大幅度提升。
◦
◦
◦
分辨率以便到达角轨迹分析，将每段信号长度减小
3 结论
为 20 s，图 10 是 CBF 和 CBF-ALE、CBF-FALE 处
理后的到达角历程图，其中图 10(a)∼(c) 为 144 Hz
本文提出了一种基于 CBF 和ALE 的空时频域
线谱的历程图，该线谱的能量较大；图 10(d)∼(f)
联合的线谱增强方法，并基于计算效率和计算精确
为 160 Hz 线谱的历程图，该线谱的能量较小，滤 度的要求，分析了不同参数对计算精确度的影响，同
波阶数取 1250。通过 CBF 的历程图可以看到，该 时引入了FALE算法提升计算效率，得出结论如下：
时间段在 90 ∼ 10 的方向上存在着连续的强宽带 (1) 结合多个维度的基于 CBF 和 ALE 的算法
◦
◦
干扰，144 Hz 和 160 Hz 线谱均受到了干扰，这就 能够从空域和时频域两方面处理信号，从而更显著
导致线谱的真实到达角难以准确分辨，在 CBF 基 地提高信号的频域信噪比。
础上对信号进行 ALE 的空时频域联合处理方法能 (2) ALE 算法中收敛步长和滤波阶数是很重要
够有效改善这个问题，从图中可以看到 CBF-ALE、 的参数，在合理情况下，滤波阶数越大，则滤波器效
CBF-FALE算法均能对3根线谱的历程图中的宽带 果越好。
强干扰进行抑制，对真实轨迹进行增强，对于能量 (3) FALE 算法相比于传统 ALE 算法能够显著
较高的 144 Hz 线谱信号或是能量较低的 160 Hz 线 提高运算效率，且在滤波阶数较大时 FALE 对计算
谱，在 25 min 前的轨迹均能够被有效地提取出来， 效率的提升更为明显，能够优化传统ALE算法在工
且其余背景噪声也得到了抑制。而在计算效率方 程应用上效率较低的不足。