Page 213 - 《应用声学》2025年第3期

第 44 卷 第 3 期 王铁成等： 结合随钻声波与密度测井的孔隙压力预测方法 747

GRNN 模型分为输入层、隐含层、求和层和输 本文对比了不同测井数据对结果训练优化的
出层。本文在求取地层压力过程中，主要的输入元 影响，如图 4 所示。图 4(a) 为结合了密度测井数据
素为深度、密度、声波、自然伽马及地层电阻率等基 及声波测井数据的地层压力系数计算结果 (本文方
本数据。在将所有输入数据进行标准化处理后输入 法)，图4(b)为通过 GRNN模型，仅利用声波测井数
模型中，最后传递至隐含层中。隐含层、求和层及输 据开展地层压力计算。对比可见通过多测井数据开
入层的处理参考相关文献[14]。 展训练优化在较短时间内就能达到较理想的优化
结果。这是由于通过密度测井及声波测井得到的地
2 评价结果 层压力对伊顿常数等关键参数产生了耦合影响作

用，进一步促进结果的准确获取。仅通过声波测井
2.1 关键参数训练优化
数据计算地层压力过程中，相同迭代次数下得到的
浙江油田 ZT 地区龙马溪组地层页岩气储量丰 压力系数计算结果与实测地层压力系数之间的误
富，但区块内地层压力异常分布，常存在多种井下事 差明显大于多测井数据训练优化得到的结果误差。
故 [15−16] 。根据地层压力合理确定钻井液密度是解 这表明使用多测井数据开展地层压力预测较单一
决此类事故的关键因素。但目前通过声波测井及密 测井数据开展地层压力预测具有明显优势。
度测井等数据计算地层压力常由于伊顿常数等关
1.95
۳̆ࠛए฾̌ᄊڡࡏԍҧጇ஝ᝠካፇ౧
键计算参数难以准确选取，导致地层压力计算结果 ۳̆ܦฉ฾̌ᄊڡࡏԍҧጇ஝ᝠካፇ౧
存在一定的误差，从而影响钻井液密度的设定。 1.90 ࠄ฾ڡࡏԍҧጇ஝
本文所建立方法旨在结合密度测井数据及声
1.85
波测井等数据开展地层压力系数预测，通过部分实
测地层压力对通过密度测井数据及声波测井数据 ԍҧጇ஝ 1.80
得到的地层压力进行优化，在按照经验值给出相关
参数初始值的情况下，不断迭代优化伊顿常数等关 1.75
键系数，从而对地层压力系数计算结果进行优化。
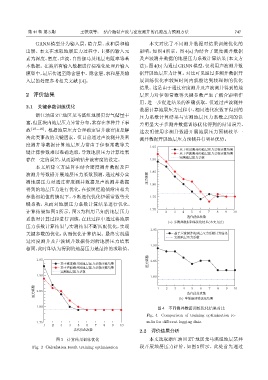
计算结果如图 3 所示，图 3 为利用已知的地层压力 1.70 1 2 3 4 5 6 7 8 9 10
ᤖ͖̽ӑ൓஝
系数对计算过程进行训练，在此过程中通过将地层
(a) ܳ฾̌஝૶ᝫጷ͖ӑፇ౧(వ஡வข)
压力系数计算结果与实测结果不断匹配优化，实现
1.95
关键参数的优化，从而优化计算结果。最终实现通 ۳̆ܦฉ฾̌ᄊڡࡏԍҧጇ஝ᝠካፇ౧
ࠄ฾ڡࡏԍҧጇ஝
过密度测井及声波测井数据得到的地层压力结果
1.90
相同，此时即认为得到的地层压力是最终的求取值。

1.95 1.85
۳̆ࠛए฾̌ᄊڡࡏԍҧጇ஝ᝠካፇ౧ ԍҧጇ஝
۳̆ܦฉ฾̌ᄊڡࡏԍҧጇ஝ᝠካፇ౧
ࠄ฾ڡࡏԍҧጇ஝
1.90
1.80
ԍҧጇ஝ 1.85 1 2 3 4 ᤖ͖̽ӑ൓஝ 7 8 9 10
6
5
(b) ӭ஝૶ᝫጷ͖ӑፇ౧
1.80
图 4 不同测井数据训练优化结果对比
Fig. 4 Comparison of training optimization re-
1.75 sults for different logging data
1 2 3 4 5 6 7 8 9 10
ᤖ͖̽ӑ൓஝ 2.2 评价结果分析

图 3 计算结果训练优化 本文选取浙江油田 ZT 地区龙马溪组地层某井
Fig. 3 Calculation result training optimization 段开展地层压力评价，如图 5 所示。此处首先通过